题目内容
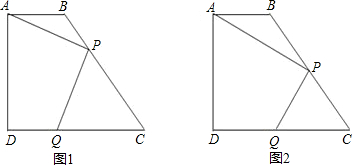
如图,在梯形ABCD中,AB∥CD,AB=2,AD=4,tanC=
,∠ADC=∠DAB=90°,P是腰BC上一个动点(不含点B、C),作PQ⊥AP交CD于点Q.(图1)
(1)求BC的长与梯形ABCD的面积;
(2)当PQ=DQ时,求BP的长;(图2)
(3)设BP=x,CQ=y,试求y关于x的函数解析式,并写出定义域.
| 4 |
| 3 |
(1)求BC的长与梯形ABCD的面积;
(2)当PQ=DQ时,求BP的长;(图2)
(3)设BP=x,CQ=y,试求y关于x的函数解析式,并写出定义域.

(1)作BH⊥CD,垂足为H,(1分)
则四边形ABHD为矩形;
∴BH=DA=4,DH=AB=2;(1分)
在Rt△BCH中,tanC=
,
∴CH=
=3,(1分)BC=
=5;(1分)
又CD=CH+DH=5,
∴S梯形ABCD=
(AB+CD)AD=14;(1+1=2分)
(2)连接AQ,
由DQ=PQ,可知△ADQ≌△APQ,AP=AD=4;(1分)
作PE⊥AB交AB的延长线于点E,(1分)
在Rt△BPE中,tan∠PBE=tanC=
,
令BE=3k,PE=4k.
则在Rt△APE中,AP2=AE2+PE2,(1分)
即42=(2+3k)2+(4k)2,解得:k=
;(1分)
∴BP=
=5k=
;(1分)
(3)作PF⊥CD交CD于点F,
由∠AEF=∠EFD=∠APQ=90°,
可得:△AEP∽△PFQ;
∴
=
,即
=
,
化简得:QF=
;(1分)
又CF=
PF=3-
x,
∴y=CF+FQ=(3-
x)+
=
;(1分)
定义域为(0<x<5).(1分)

则四边形ABHD为矩形;
∴BH=DA=4,DH=AB=2;(1分)
在Rt△BCH中,tanC=
| 4 |
| 3 |
∴CH=
| BH |
| tanC |
| BH2+CH2 |
又CD=CH+DH=5,
∴S梯形ABCD=
| 1 |
| 2 |
(2)连接AQ,
由DQ=PQ,可知△ADQ≌△APQ,AP=AD=4;(1分)
作PE⊥AB交AB的延长线于点E,(1分)
在Rt△BPE中,tan∠PBE=tanC=
| 4 |
| 3 |
令BE=3k,PE=4k.
则在Rt△APE中,AP2=AE2+PE2,(1分)
即42=(2+3k)2+(4k)2,解得:k=
4
| ||
| 25 |
∴BP=
| BE2+PE2 |
4
| ||
| 5 |
(3)作PF⊥CD交CD于点F,
由∠AEF=∠EFD=∠APQ=90°,
可得:△AEP∽△PFQ;
∴
| QF |
| PF |
| EP |
| AE |
| QF | ||
4-
|
| ||
2+
|
化简得:QF=
| 80x-16x2 |
| 50+15x |
又CF=
| 3 |
| 4 |
| 3 |
| 5 |
∴y=CF+FQ=(3-
| 3 |
| 5 |
| 80x-16x2 |
| 50+15x |
| -5x2+19x+30 |
| 3x+10 |
定义域为(0<x<5).(1分)


练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
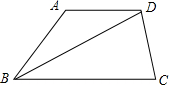


 从B、D同时出发,当其中一个点到达点A时,另一点也随之停止移动.设移动时间为t(s).
从B、D同时出发,当其中一个点到达点A时,另一点也随之停止移动.设移动时间为t(s). 形铁片的另一底边比AB长10cm.
形铁片的另一底边比AB长10cm.