题目内容
【题目】△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm,2cm,2cmB.3cm,3cm,3cmC.4cm,4cm,4cmD.2cm,3cm,5cm
【答案】A
【解析】
连接OA,OB,OC,利用角的平分线上的点到角的两边的距离相等可知△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,所以BD=BF,CD=CE,AE=AF,又因为点O到三边AB、AC、BC的距离是CD,所以AB=8-CD+6-CD=10,解得CD=2,所以点O到三边AB、AC、BC的距离为2.
连接OA,OB,OC,则△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,
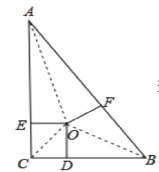
∴BD=BF,CD=CE,AE=AF,
又∵∠C=90°,OD⊥BC于D,OE⊥AC于E,且O为△ABC三条角平分线的交点
∴四边形OECD是正方形,
则点O到三边AB、AC、BC的距离=CD,
∴AB=8CD+6CD=2CD+14,又根据勾股定理可得:AB=10,
即2CD+14=10
∴CD=2,
即点O到三边AB、AC、BC的距离为2cm.
故选A

练习册系列答案
相关题目