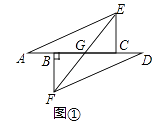
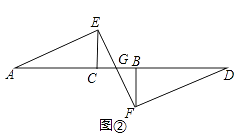
题目内容
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
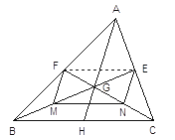
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
【答案】(1)是; (2)①平行; ②1; ③![]() ; ④16。
; ④16。
【解析】(1)三角形的中线相交于一点,所以H为BC的中点.
(2)①
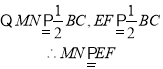
![]() 四边形EFMN 是平行四边形
四边形EFMN 是平行四边形
②当![]() 时,四边形EFMN 是矩形
时,四边形EFMN 是矩形
此时, ![]() 垂直平分
垂直平分![]()
![]()
![]()
![]()
③当![]() 时,四边形EFMN 是菱形
时,四边形EFMN 是菱形
即![]()
![]()
④![]() AB=10,BC=16, AB=AC
AB=10,BC=16, AB=AC
![]()
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目