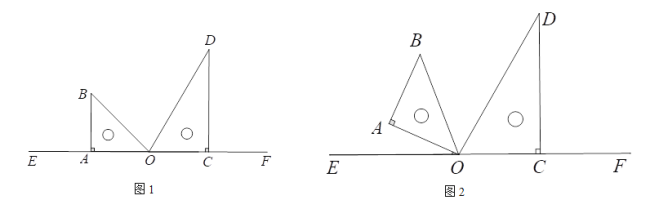题目内容
【题目】在平面直角坐标系xOy中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,对于
,对于![]() 的横长、纵长、纵横比给出如下定义:
的横长、纵长、纵横比给出如下定义:
将![]() 中的最大值,称为
中的最大值,称为![]() 的横长,记作
的横长,记作![]() ;将
;将![]() 中的最大值,称为
中的最大值,称为![]() 的纵长,记作
的纵长,记作![]() ;将
;将![]() 叫做
叫做![]() 的纵横比,记作
的纵横比,记作![]() .
.
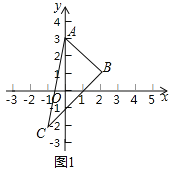
例如:如图![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,则
,则![]() ,
,
所以![]() .
.
![]() 如图2,点
如图2,点![]() ,
,
![]() 点
点![]() ,
,
则![]() 的纵横比
的纵横比![]() ______
______
![]() 的纵横比
的纵横比![]() ______;
______;
![]() 点F在第四象限,若
点F在第四象限,若![]() 的纵横比为1,写出一个符合条件的点F的坐标;
的纵横比为1,写出一个符合条件的点F的坐标;
![]() 点M是双曲线
点M是双曲线![]() 上一个动点,若
上一个动点,若![]() 的纵横比为1,求点M的坐标;
的纵横比为1,求点M的坐标;
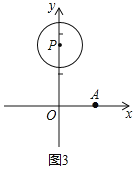
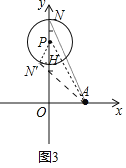
![]() 如图3,点
如图3,点![]() 以
以![]() 为圆心,1为半径,点N是
为圆心,1为半径,点N是![]() 上一个动点,直接写出
上一个动点,直接写出![]() 的纵横比
的纵横比![]() 的取值范围.
的取值范围.
【答案】 ![]() 1
1
【解析】分析:(1)①根据纵横比的定义计算即可;
②点F在第四象限的角平分线上即可;
③分三种情形讨论即可.
(2)如图3中,当当![]() 时,可得
时,可得![]() 的纵横比
的纵横比![]() 的最大值
的最大值![]() ,
,
当![]() 与
与![]() 相切时,切点在第二象限时,可得
相切时,切点在第二象限时,可得![]() 的纵横比
的纵横比![]() 的最小值.
的最小值.
详解:![]()
由题意![]() 的纵横比
的纵横比![]() 的纵横比
的纵横比![]() ,
,
故答案为![]() .
.
![]() 由点F在第四象限,若
由点F在第四象限,若![]() 的纵横比为1,则
的纵横比为1,则![]() 在第四象限的角平分线上即可
在第四象限的角平分线上即可![]() .
.
![]() 如图设
如图设![]()
a、当![]() 时,点M在
时,点M在![]() 上,则
上,则![]() ,
,
此时![]() 的横长
的横长![]() 的纵长为
的纵长为![]() ,
,
![]() 的纵横比为1,
的纵横比为1,
![]() ,
,
![]() 或
或![]() 舍弃
舍弃![]() ,
,
![]() ,
,
![]() .
.
b、当![]() 时,点M在
时,点M在![]() 上,则
上,则![]() ,
,
此时![]() 的横长
的横长![]() 的纵长为
的纵长为![]() ,
,
![]() 的纵横比为1,
的纵横比为1,
![]() ,
,
![]()
![]() 舍弃
舍弃![]() ,
,
c、当![]() 时,点M在
时,点M在![]() 上,则
上,则![]() ,
,
此时![]() 的横长
的横长![]() 的纵长为
的纵长为![]() ,
,
![]() 的纵横比为1,
的纵横比为1,
![]() ,
,
![]() 或
或![]() 舍弃
舍弃![]() ,
,
![]() ,
,
![]() ,
,
综上所述,点M坐标为![]() 或
或![]()
![]() 如图3中,当
如图3中,当![]() 时,可得
时,可得![]() 的纵横比
的纵横比![]() 的最大值
的最大值![]() ,
,
当![]() 与
与![]() 相切时,切点在第二象限时,可得
相切时,切点在第二象限时,可得![]() 的纵横比
的纵横比![]() 的最小值,
的最小值,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,易知
,易知![]() ,作
,作![]() 于H.
于H.
![]() ,
,
![]() ,
,
此时![]() 的纵横比
的纵横比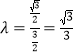 ,
,
![]() .
.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】方程是刻画现实世界的有效模型,表格是建立方程的策略之一.请填写表格数据,并列方程解决问题.轮船和汽车都从甲地开往乙地,海路比公路近40千米,轮船上午7点开出,速度是每小时24千米.汽车上午10点开出,速度为每小时40千米,结果同时到达了乙地.求甲、乙两地的海路和公路长.
速度 | 时间 | 路程 | |
汽车 | 40 |
| x |
轮船 | 24 |
|
|
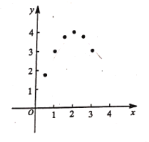
【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大请将他们的探究过程补充完整。
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=_________。
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | ... | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | ... |
y | ... | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | ... |
写出m=__________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得:x=_______时,矩形的面积最大: 写出该函数的其它性质(一条即可):_______________________________________.