题目内容
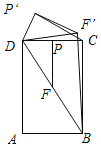
【题目】在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.
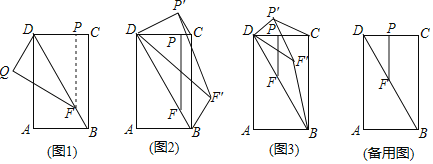
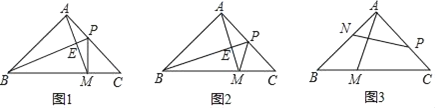
(1)如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;
(2)如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.
【答案】(1)证明见解析;(2)①证明见解析;②![]() 或
或![]() .
.
【解析】(1)根据翻折的性质以及平行线的性质可知∠DFQ=∠ADF,所以△DEF是等腰三角形;
(2)①由于PF∥BC,所以△DPF∽△DCB,从而易证△DP′F′∽△DCB;
②由于△DF'B是直角三角形,但不知道哪个的角是直角,故需要对该三角形的内角进行分类讨论.
(1)由翻折可知:∠DFP=∠DFQ,
∵PF∥BC,
∴∠DFP=∠ADF,
∴∠DFQ=∠ADF,
∴△DEF是等腰三角形;
(2)①若0°<α<∠BDC,即DF'在∠BDC的内部时,
∵∠P′DF′=∠PDF,
∴∠P′DF′﹣∠F′DC=∠PDF﹣∠F′DC,
∴∠P′DC=∠F′DB,
由旋转的性质可知:△DP′F′≌△DPF,
∵PF∥BC,
∴△DPF∽△DCB,
∴△DP′F′∽△DCB
∴![]() ,
,
∴△DP'C∽△DF'B;
②当∠F′DB=90°时,如图所示,
∵DF′=DF=![]() BD,
BD,
∴![]() ,
,
∴tan∠DBF′=![]() ;
;
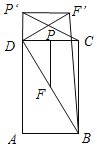
当∠DBF′=90°,此时DF′是斜边,即DF′>DB,不符合题意;
当∠DF′B=90°时,如图所示,
∵DF′=DF=![]() BD,
BD,
∴∠DBF′=30°,
∴tan∠DBF′=![]() .
.

【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
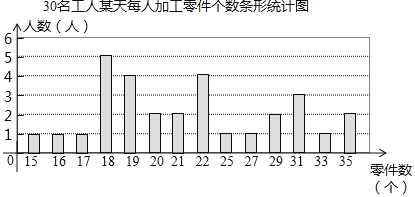
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.