题目内容
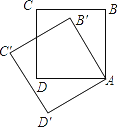
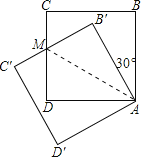
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】设CD、B′C′相交于点M,连结AM,根据旋转角的定义易得:∠BAB′=30°,根据HL易得△AB′M≌△ADM,所以公共部分面积等于△ADM面积的2倍;
设DM=x,在△AMD中利用勾股定理求得DM,进而解答即可.
设CD、B′C′相交于点M,连结AM,设DM=x,根据旋转的性质以及正方形的性质可得AB′=AD,AM=AM,∠BAB′=30°,∠B′=∠D=90°.
∵AB′=AD,AM=AM,
∴△AB′M≌△ADM.
∵∠BAB′=30°,
∴∠MAD=30°, AM=2x.
∵x2+1=4x2,
∴x=![]() ,
,
∴SADM′=![]() ,
,
∴重叠部分的面积SADMB′=![]() =
=![]() .
.
故选B.

练习册系列答案
相关题目