题目内容
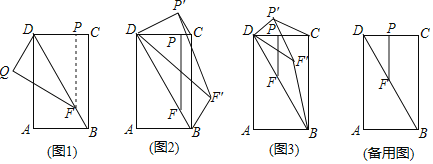
【题目】如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.
(1)求景点B与C的距离;
(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
【答案】(1)10km;(2)![]() km.
km.
【解析】(1)先根据方向角的定义得出∠CAB=30°,∠ABC=120°,由三角形内角和定理求出∠C=180°﹣∠CAB﹣∠ABC=30°,则∠CAB=∠C=30°,根据等角对等边求出BC=AB=10km;
(2)首先过点C作CE⊥AB于点E,然后在Rt△CBE中,求得答案即可.
(1)如图,由题意得∠CAB=30°,∠ABC=90°+30°=120°,
∴∠C=180°﹣∠CAB﹣∠ABC=30°,
∴∠CAB=∠C=30°,
∴BC=AB=10km,
即景点B、C相距的路程为10km;
(2)如图,过点C作CE⊥AB于点E,
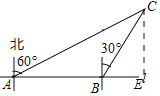
∵BC=10km,C位于B的北偏东30°的方向上,
∴∠CBE=60°,
在Rt△CBE中,CE=![]() BC=5
BC=5![]() km.
km.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目