题目内容
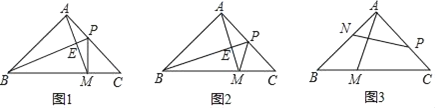
【题目】在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点P为AC上一点，M为BC上一点．
（1）若AM⊥BP于点E．
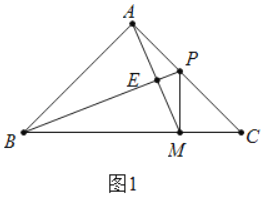
①如图1，BP为△ABC的角平分线，求证：PA＝PM；
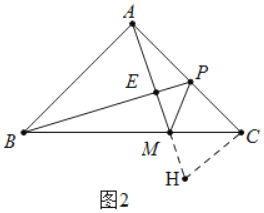
②如图2，BP为△ABC的中线，求证：BP＝AM+MP．
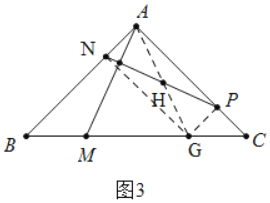
（2）如图3，若点N在AB上，AN＝CP，AM⊥PN，求
的值．
【答案】（1）①详见解析；②详见解析；（2）1.
【解析】
（1）①只要证明
，利用角平分线的性质定理即可解决问题；
②作
交
的延长线于
．只要证明
，
，即可解决问题；
（2）如图3中，作
交
于
，连接
，
交于点．首先证明四边形
是矩形，推出
，
，再证明
，可得
，推出
即可解决问题；
（1）①证明：如图1中，
，
，
，
平分
，
，
，
，
，
，
，
，
垂直平分线段，
，
，
，
，
，
，
平分，
．
②如图2中，作交的延长线于．
，
，
，
，
，
，
，
，
，
，
，
，
．
（2）解：如图3中，作交于，连接，交于点．
，
，
，
，
，
，
，
四边形是平行四边形，
，
四边形是矩形，
，，
，
，
，
，
，
，
，
，
．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
