题目内容
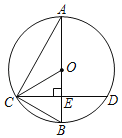
【题目】如图,菱形ABCD中,AB=5,连接BD,sin∠ABD=![]() ,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
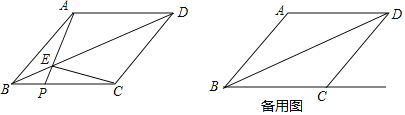
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=n(0<n<5),求△PEC的面积;(用含n的代数式表示)
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,请直接写出BP的长.
【答案】(1)见解析;(2)![]() (0<n<5);(3)线段BP的长为
(0<n<5);(3)线段BP的长为![]() 或15
或15
【解析】
(1)由菱形的性质得出BA=BC,∠ABD=∠CBD.由SAS证明△ABE≌△CBE,即可得出结论.
(2)连结AC,交BD于点O,过点A作AH⊥BC于H,过点E作EF⊥BC于F,由菱形的性质得出AC⊥BD.由三角函数求出AO=OC=![]() ,BO=OD=2
,BO=OD=2![]() .由菱形面积得出AH=4,BH=3.由相似三角形的性质得出
.由菱形面积得出AH=4,BH=3.由相似三角形的性质得出![]() =
=![]() ,求出EF的长,即可得出答案.
,求出EF的长,即可得出答案.
(3)因为点P在线段BC的延长线上,所以∠EPC不可能为直角.分情况讨论:①当∠ECP=90°时,②当∠CEP=90°时,由全等三角形的性质和相似三角形的性质即可得出答案.
(1)∵四边形ABCD是菱形,
∴BA=BC,∠ABE=∠CBE.
在△ABE和△CBE中,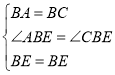 ,
,
又∵BE=BE,
∴△ABE≌△CBE
∴AE=CE.
(2)连接AC,交BD于点O,过点A作AH⊥BC,过点E作EF⊥BC,如图1所示,垂足分别为点H、F.
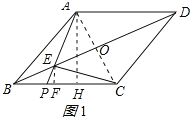
∵四边形ABCD是菱形,
∴AC⊥BD.
∵AB=5,sin∠ABD=![]() ,
,
∴AO=OC=![]() ,BO=OD=2
,BO=OD=2![]() .
.
∵![]() ACBD=BCAH,
ACBD=BCAH,
∴AH=4,BH=3.
∵AD∥BC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵EF∥AH,
∴![]() =
=![]() ,
,
∴EF=![]() ,
,
∴y=![]() PCEF=
PCEF=![]()
![]() (5﹣n)=
(5﹣n)=![]() (0<n<5).
(0<n<5).
(3)因为点P在线段BC的延长线上,所以∠EPC不可能为直角.如图2所示:
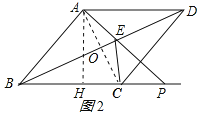
①当∠ECP=90°时
∵△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∵cos∠ABP=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BP=![]() ;
;
②当∠CEP=90°时,
∵△ABE≌△CBE,
∴∠AEB=∠CEB=45°,
∴AO=OE=![]() ,
,
∴ED=![]() ,BE=3
,BE=3![]() .
.
∵AD∥BP,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BP=15.
综上所述,当△EPC是直角三角形时,线段BP的长为![]() 或15.
或15.