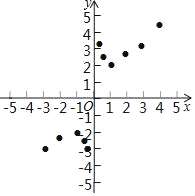题目内容

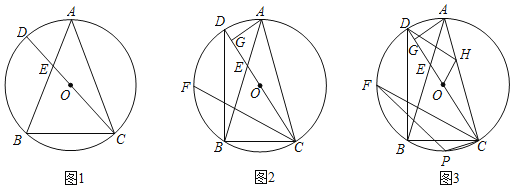
【题目】已知：等边△ABC，点P是直线BC上一点，且PC:BC=1:4,则tan∠APB=_______，

【答案】或．

【解析】

过A作AD⊥BC于D，设等边△ABC的边长为4a，则DC=2a，AD=2a，PC=a，分类讨论：当P在BC的延长线上时，DP=DC+CP=2a+a=3a；当P点在线段BC上，即在P′的位置，则DP′=DC-CP′=a，然后分别利用正切的定义求解即可．

解：如图，过A作AD⊥BC于D，

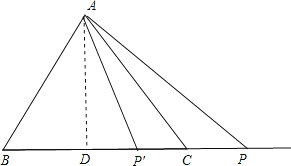
设等边△ABC的边长为4a，则DC=2a，AD=2a，PC=a，

当P在BC的延长线上时，DP=DC+CP=2a+a=3a，

在Rt△ADP中，tan∠APD=；

当P点在线段BC上，即在P′的位置，则DP′=DC-CP′=a，

在Rt△ADP′中，tan∠AP′D=．

故答案为：或．

练习册系列答案
相关题目

【题目】已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．

（1）如图（1），连接AF、CE．

①四边形AFCE是什么特殊四边形？说明理由；

②求AF的长；

（2）如图（2），动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

【题目】如图，点的坐标为，点，分别在轴，轴的正半轴上运动，且，下列结论：

①

②当时四边形是正方形

③四边形的面积和周长都是定值

④连接，，则，其中正确的有（ ）

A.①②B.①②③C.①②④D.①②③④

【题目】如图，已知抛物线y=－x2+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=－x+3交于C、D两点．连接BD、AD．

（1）求m的值．

（2）抛物线上有一点P，满足S△ABP=4S△ABD，求点P的坐标．

【题目】某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球，学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计，制成了两幅不完整的统计图(图(1)和图(2))：

(1)请你求出该班的总人数，并补全条形图(注：在所补小矩形上方标出人数)；

(2)在该班团支部4人中，有1人选修排球，2人选修羽毛球，1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人，那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少？

【题目】已知：内接于⊙，连接并延长交于点，交⊙于点，满足．

（1）如图1，求证：；

（2）如图2，连接，点为弧上一点，连接，=，过点作，垂足为点，求证：；

（3）如图3，在（2）的条件下，点为上一点，分别连接，，过点作，交⊙于点，，，连接，求的长．

【题目】如图，菱形ABCD中，AB＝5，连接BD，sin∠ABD＝，点P是射线BC上一点（不与点B重合），AP与对角线BD交于点E，连接EC．

（1）求证：AE＝CE；

（2）当点P在线段BC上时，设BP＝n（0＜n＜5），求△PEC的面积；（用含n的代数式表示）

（3）当点P在线段BC的延长线上时，若△PEC是直角三角形，请直接写出BP的长．

【题目】小明根据学习函数的经验，对函数y=x+的图象与性质进行了探究．

下面是小明的探究过程，请补充完整：

（1）函数y=x+的自变量x的取值范围是_____．

（2）下表列出了y与x的几组对应值，请写出m，n的值：m=_____，n=_____；

x

…

﹣3

﹣2

﹣1

﹣

﹣

1

2

3

4

…

y

…

﹣

﹣

﹣2

﹣

﹣

m

2

n

…

（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

（4）结合函数的图象，请完成：

①当y=﹣时，x=_____．

②写出该函数的一条性质_____．

③若方程x+=t有两个不相等的实数根，则t的取值范围是_____．

【题目】如图，已知正方形ABCD的边长是8，点E是AB边上一动点，连接CE，过点B作BG⊥CE于点G，点P是AB边上另一动点，则PD+PG的最小值是（ ）

A.B.C.D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网