Question

【题目】已知：如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论：①DF⊥AB;②CG=3GA;③CG=DF+GE;④S四边形BFGC=1中,说法正确的是( )

A. ①③④B. ②③C. ①③D. ①②③

Answer 1

【答案】C

【解析】

①由四边形ABCD是菱形，得出对角线平分对角，求得∠GAD=∠2，得出AG=GD，AE=ED，由SAS证得△AFG≌△AEG，得出∠AFG=∠AEG=90°，即可得出①正确；

②由DF⊥AB，F为边AB的中点，证得AD=BD，证出△ABD为等边三角形，得出∠BAC=∠1=∠2=30°，由AC=2ABcos∠BAC，AG= ，求出AC，AG，即可得出②不正确；

③由勾股定理求出DF= ，由GE=tan∠2ED求出GE，即可得出③正确；

④由S四边形BFGC=S△ABC-S△AGF求出数值，即可得出④不正确．

∵四边形ABCD是菱形，
∴∠FAG=∠EAG，∠1=∠GAD，AB=AD，
∵∠1=∠2，
∴∠GAD=∠2，
∴AG=GD，
∵GE⊥AD，
∴GE垂直平分AD，
∴AE=ED，
∵F为边AB的中点，
∴AF=AE，
在△AFG和△AEG中，

，
∴△AFG≌△AEG（SAS），
∴∠AFG=∠AEG=90°，
∴DF⊥AB，
∴①正确；

连接BD.

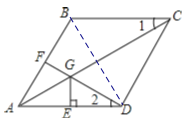
∵DF⊥AB，F为边AB的中点，
∴AF=AB=1，AD=BD，
∵AB=AD，
∴AD=BD=AB，
∴△ABD为等边三角形，
∴∠BAD=∠BCD=60°，
∴∠BAC=∠1=∠2=30°，
∴AC=2ABcos∠BAC=2×2×，
AG= ，
∴CG=AC-AG= ，
∴CG=2GA，
∴②不正确；
∵GE垂直平分AD，
∴ED=AD=1，
由勾股定理得：DF= ，
GE=tan∠2ED=tan30°×1= ，
∴DF+GE=

∴③正确；
∵∠BAC=∠1=30°，
∴△ABC的边AC上的高等于AB的一半，即为1，
FG= ，
S四边形BFGC=S△ABC-S△AGF= ，
∴④不正确；
故选：C