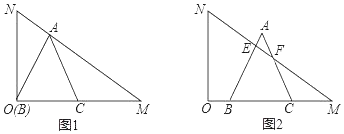题目内容
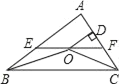
【题目】等腰△ABC中,AB=BC=8,∠ABC=120°,BE是∠ABC的平分线,交AC于E,点D是AB的中点,连接DE,作EF∥AB于点F.
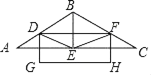
(1)求证四边形BDEF是菱形;
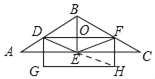
(2)如图以DF为一边作矩形DFHG,且点E是此矩形的对称中心,求矩形另一边的长.
【答案】(1)见解析;(2)FH=4.
【解析】
(1)先证明四边形BDEF是平行四边形,再根据DE=![]() AB=BD,即可得到四边形BDEF是菱形;
AB=BD,即可得到四边形BDEF是菱形;
(2)先证明四边形BEFH是平行四边形,得到BE=FH,再根据BE=![]() BC=4,即可得到FH=4.
BC=4,即可得到FH=4.
解:(1)∵AB=BC,BE是∠ABC的平分线,
∴E是AC的中点,且BE⊥AC,
又∵点D是AB的中点,
∴DE是△ABC的中位线,
∴DE∥BF,
又∵EF∥BD,
∴四边形BDEF是平行四边形,
又∵Rt△ABE中,点D是AB的中点,
∴DE=![]() AB=BD,
AB=BD,
∴四边形BDEF是菱形;
(2)连接EH,
∵点E是此矩形的对称中心,
∴D,E,H在同一直线上,
∵DE∥BF,
∴EH∥BF,
∵AB=BC,BE是∠ABC的角平分线,
∴点E是AC的中点,且BE⊥AC,
∵EF∥AB,
∴点F是BC的中点,
∵点D是AB的中点,
∴DF∥AC,
∴BE⊥DF,
又∵DFHG是矩形,
∴FH⊥DF,
∴BE∥FH,
∴四边形BEHF是平行四边形,
∴BE=FH,
∵∠ABC=120°,BE平分∠ABC,
∴∠EBF=60°,
又∵∠BEC=90°,
∴∠C=30°,
∴BE=![]() BC=4,
BC=4,
∴FH=4.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.