题目内容
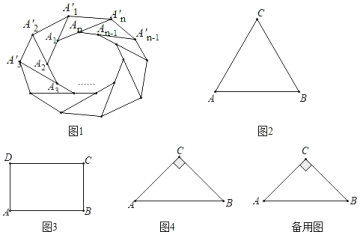
【题目】定义:按螺旋式分别延长n边形的n条边至一点,若顺次连接这些点所得的图形与原多边形相似,则称它为原图形的螺旋相似图形.例如:如图1,分别延长多边形A1A2…An的边得A1′,A2′,…,An′,若多边形A1′A2′…An′与多边形A1A2…An相似,则多边形A1′A2′…An′就是A1A2…An的螺旋相似图形.
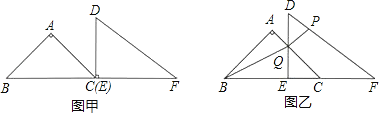
(1)如图2,已知△ABC是等边三角形,作出△ABC的一个螺旋相似图形,简述作法,并给以证明.
(2)如图3,已知矩形ABCD,请探索矩形ABCD是否存在螺旋相似图形,若存在,求出此时AB与BC的比值;若不存在,说明理由.
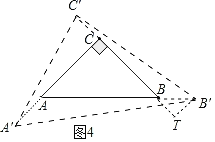
(3)如图4,△ABC是等腰直角三角形,AC=BC=2,分别延长CA,AB,BC至A′,B′,C′,使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC,请直接写出BB′,CC′的长(用含k的代数式表示)
【答案】(1)见解析;(2)AB:BC=1;(3)BB′=![]() k,CC′=k.
k,CC′=k.
【解析】
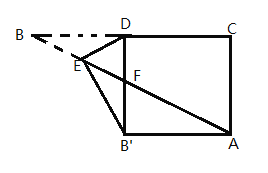
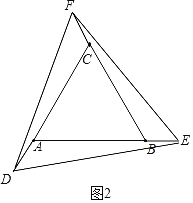
(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形,证明△DEF是等边三角形即可解决问题.
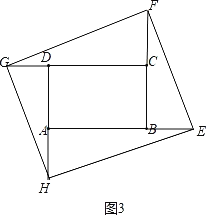
(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.分两种情形,利用相似三角形的性质以及相似矩形的性质,构建关系式证明a=b即可解决问题.
(3)如图4中,作B′T⊥CB交CB的延长线于T.设TB=TB′=m,证明△A′CC′≌△A′TB′(ASA),推出A′C=TC′,CC′=TB′=BT,构建关系式推出m=k即可解决问题.
解:(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形.
理由:∵△ABC是等边三角形,
∴AB=BC=AC,∠CAB=∠ABC=∠ACB,
∴∠DAE=∠FCD=∠EBF=120°,
∵BE=CF=AD,
∴CD=AE=BF,
∴△FCD≌△DAE≌△EBF(SAS),
∴DF=DE=EF,
∴△DEF是等边三角形,
∴△DEF∽△ABC,
∴△DEF是△ABC的一个螺旋相似图形.
(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.
由题意:△BEF∽△AHE,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
当![]() =
=![]() =
=![]() 时,
时,![]() =
=![]() =
=![]() ,
,
∴x=![]() y,ax+x2=by+y2,
y,ax+x2=by+y2,
∴by+![]() y2=by+y2,
y2=by+y2,
∴a2=b2,
∴a=b,即AB:BC=1.
当![]() =
=![]() =
=![]() 时.
时.![]() =
=![]() =
=![]() ,
,
∴x=![]() y,ax+x2=by+y2,
y,ax+x2=by+y2,
∴![]() y+
y+![]() y2=by+y2,
y2=by+y2,
∴![]() y(1+
y(1+![]() )=0,
)=0,
∵y≠0,1+![]() ≠0,
≠0,
∴a2=b2,
∴a=b,即AB:BC=1,
综上所述,AB:BC=1.
(3)如图4中,作B′T⊥CB交CB的延长线于T.
∵AC=BC=2,∠ACB=90°,
∴∠ABC=∠CAB=45°,
∴∠TBB′=∠ABC=45°,
∴∠TB′B=∠TBB′=45°,
∴TB=TB′,设TB=TB′=m,
∵△A′B′C′是△ABC的螺旋相似三角形,
∴A′C′=B′C′,∠A′C′B′/span>=90°,
∵∠A′C′C+∠B′C′=90°,∠A′CC+∠C′A′C=90°,
∴∠C′A′C=∠B′C′T,
∵∠A′CC′=∠T=90°,
∴△A′CC′≌△A′TB′(ASA),
∴A′C=TC′,CC′=TB′=BT,
∴2+2k=2+2m,
∴m=k,
∴BB′=![]() k,CC′=k.
k,CC′=k.

 阅读快车系列答案
阅读快车系列答案