题目内容
【题目】D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点，O是△ABC所在平面上的动点，连接OB，OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．
（1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；
（2）若四边形DGFE是菱形，点O所在位置应满足什么条件？（直接写出答案不需要说明理由．）
（3）在图2中作出点O，使得四边形DGFE是正方形（保留作图痕迹，不写作法）．
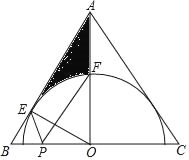
【答案】（1）见解析；（2）当点O在以A为圆心，BC为半径的圆上时，四边形DGFE是菱形；（3）如图2，点O即为所求，见解析．
【解析】
（1）由三角形的中位线定理证DE=
BC，DE∥BC，GF=BC，GF∥BC，则可得到DE=GF，DE∥GF，由平行四边形的判定即可证明结论；
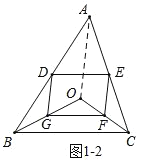
（2）当点O在以A为圆心，BC为半径的圆上时，四边形DGFE是菱形，如图1-2，连接AO，因为当点O在以A为圆心，BC为半径的圆上时，AO=BC，由三角形的中位线定理可证DG=GF=EF=DE，即可得出四边形DGEF为菱形；
（3）在满足（2）的条件下，只要AO⊥BC，即可证四边形DGEF是正方形，过
作
的垂线AM，在AM上截取AO，使AO=BC即可得到答案．
（1）证明：∵D、E分别是不等边三角形ABC的边AB、AC的中点，
∴DE＝BC，DE∥BC，
∵点G、F分别是OB、OC的中点，
∴GF＝BC，GF∥BC，
∴DE＝GF，DE∥GF，
∴四边形DGFE是平行四边形；
（2）解：当点O在以A为圆心，BC为半径的圆上时，四边形DGFE是菱形，理由如下：
如图1﹣2，连接AO，
当点O在以A为圆心，BC为半径的圆上时，AO＝BC，
∵D是AB的中点，G是OB的中点，
∴DG＝AO，
同理，EF＝AO，
∴DG＝EF＝AO，
∵AO＝BC，且由（1）知GF＝DE＝BC，
∴DG＝GF＝EF＝DE，
∴四边形DGEF为菱形；
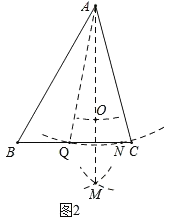
（3）解：如图2，点O即为所求，作法如下：
①在线段BC上取点Q，以A为圆心，AQ的长为半径画弧，交线段BC于点N；
②分别以Q，N为圆心，大于QN长度为半径画弧，两弧交于点M；
③连接AM，在AM上截取AO，使AO＝BC．
