题目内容
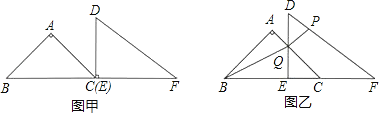
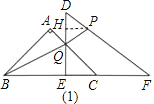
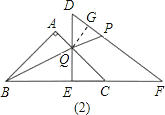
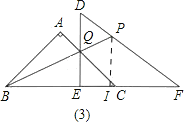
【题目】已知:把Rt△ABC和Rt△DEF按如图甲摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠BAC=∠DEF=90°,∠ABC=45°,BC=9cm,DE=6cm,EF=8cm.如图乙,△DEF从图甲的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△DEF的顶点F出发,以3cm/s的速度沿FD向点D匀速移动.当点P移动到点D时,P点停止移动,△DEF也随之停止移动.DE与AC相交于点Q,连接BQ、PQ,设移动时间为t(s).解答下列问题:
(1)设三角形BQE的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围;
(2)当t为何值时,三角形DPQ为等腰三角形?
(3)是否存在某一时刻t,使P、Q、B三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
【答案】(1)![]() (
(![]() );(2)见解析;(3)当
);(2)见解析;(3)当![]() s,点P、Q、B三点在同一条直线上.
s,点P、Q、B三点在同一条直线上.
【解析】
试题分析:(1)在Rt△DEF中由勾股定理可以得到DF=10.同理,在Rt△ABC中,∠ABC=45°,所以△ABC为等腰直角三角形;由DE⊥BC,∠ACB=45°,知△QEC也是等腰直角三角形,所以,QE=CE=t,则BE=BC﹣CE=9﹣t;则△BQE的面积y=![]() BEQE(0<t≤
BEQE(0<t≤![]() );
);
(2)在Rt△DEF中,DE=6,DF=10,所以,cos∠D=![]() ,sin∠D=
,sin∠D=![]() ;在Rt△PDG中,通过sin∠D求得PG、cos∠D解得DG,
;在Rt△PDG中,通过sin∠D求得PG、cos∠D解得DG,
那么GQ=DQ﹣DG;在Rt△PGQ中,利用勾股定理,求得PQ2.若△DPQ为等腰三角形时,分三种情况:①若DP=DQ;②若DP=PQ;③当DQ=PQ时;
(3)①当t=0时,点B、P、Q在同一条直线上;
②当B、Q、P在同一直线上时,过点P作DE的垂线,垂足为G,则PG∥BE,△DPG∽△DFE;然后由相似三角形的对应边成比例求得 PG、DG的值,而DQ=6﹣t,所以求得GQ=DQ﹣DG的值,根据平行线的判定定理知GP∥BE,可证△GPQ∽△QBE,所以,
GP:BE=GQ:EQ,从而解得t=![]() ,点B、Q、P在同一直线上.
,点B、Q、P在同一直线上.
解:(1)∠ACB=45°,∠DEF=90°,
∴∠EQC=45°.
∴EC=EQ=t,
∴BE=9﹣t.
∴![]() ,
,
即:![]() (
(![]() )
)
(2)①当DQ=DP时,∴6﹣t=10﹣3t,解得:t=2s.
②当PQ=PD时,过P作PH⊥DQ,交DE于点H,
则DH=HQ=![]() ,由HP∥EF,
,由HP∥EF,
∴![]() 则
则 ,解得
,解得![]() s
s
③当QP=QD时,过Q作QG⊥DP,交DP于点G,
则GD=GP=![]() ,可得:△DQG∽△DFE,
,可得:△DQG∽△DFE,
∴![]() ,则
,则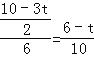 ,
,
解得![]() s
s
(3)假设存在某一时刻t,
使点P、Q、B三点在同一条直线上.
则,过P作PI⊥BF,交BF于点I,
∴PI∥DE,
于是:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,则
,则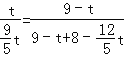 ,
,
解得:![]() s.
s.
答:当![]() s,点P、Q、B三点在同一条直线上.
s,点P、Q、B三点在同一条直线上.

 名校课堂系列答案
名校课堂系列答案