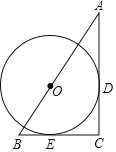题目内容
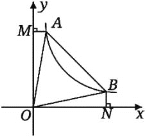
【题目】如图，正方形ABCD的顶点A，B在x轴的负半轴上，反比例函数y＝
（k1≠0）在第二象限内的图象经过正方形ABCD的顶点D（m，2）和BC边上的点G（n，
），直线y=k2x+b（k2≠0）经过点D，点G，则不等式≤k2x+b的解集为__________．
【答案】-3≤x≤-1或x＞0．
【解析】
利用正方形ABCD的顶点D的坐标得到正方形的边长为2，则G点坐标表示为（n-2，
），则根据反比例函数图象上点的坐标特征得到2m=（m-2），求出m得到G（-3，），D（-1，2），然后结合函数图象，写出一次函数图象在反比例函数图象上方所对应的自变量的范围（含两图象交点的横坐标）．
解：∵正方形ABCD的顶点D的坐标为（m，2），
∴正方形的边长为2，
∴G（n-2，），
根据题意将D（m，2），G（m-2，）代入到反比例函数y＝
（k1≠0）图象上，
∴2m=（m-2），
解得m=-1，
∴G（-3，），D（-1，2），
∵当-3≤x≤-1或x＞0时，≤k2x+b，
∴不等式≤k2x+b的解集为-3≤x≤-1或x＞0．
故答案为-3≤x≤-1或x＞0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
