��Ŀ����
����Ŀ��![]() �괺���ڼ䣬����״������Ű��ͻ�������������ô�����˲���������������۳�Ϊ���ʱ������Ҫ��һ�����۷�ʽ��ij����ó��˾��˿�����һ�����꣬���۵���ij��ũ��Ʒ����֪��ũ��Ʒ�ɱ�Ϊÿǧ��
�괺���ڼ䣬����״������Ű��ͻ�������������ô�����˲���������������۳�Ϊ���ʱ������Ҫ��һ�����۷�ʽ��ij����ó��˾��˿�����һ�����꣬���۵���ij��ũ��Ʒ����֪��ũ��Ʒ�ɱ�Ϊÿǧ��![]() Ԫ�����鷢�֣�ÿ��������
Ԫ�����鷢�֣�ÿ��������![]() �����۵���
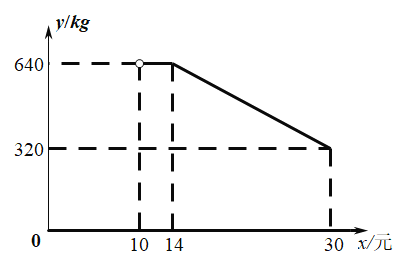
�����۵���![]() ��Ԫ��������ͼ��ʾ�ĺ�����ϵ������
��Ԫ��������ͼ��ʾ�ĺ�����ϵ������![]() ��
��
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ������Ա���
֮��ĺ�����ϵʽ������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�������۵���xΪ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
���𰸡���1��![]() ��2������Ϊ
��2������Ϊ![]() Ԫʱ��ÿ�����������������������
Ԫʱ��ÿ�����������������������![]() Ԫ
Ԫ
��������
��1����ͼ��֪����10��x��14ʱ��y��640����14��x��30ʱ����y��kx+b������14��640������30��320���ⷽ���鼴�ɵõ����ۣ�
��2����ú�������ʽΪW����x��10������20x+920������20��x��28��2+6480�����ݶ��κ��������ʼ��ɵõ����ۣ�
�⣺��1����ͼ��֪����![]() ʱ��
ʱ��![]()
��![]() ʱ����
ʱ����![]()
��![]() ��
��![]() ����
����
��![]() ��
��
���![]()
![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
����������![]()
��2����ÿ�����������ΪWԪ
��10��x��14ʱ��W��640����x��10����640x��6400��
��k��640��0��
��W����x�����������
�൱x��14ʱ��W��4��640��2560Ԫ��
��14��x��30ʱ��W����x��10������20x+920������20��x��28��2+6480��
��a����20��0����������
��W�����ֵ
��14��x��30��
�൱x��28ʱ��W�����6480
![]()
![]() ��x��28ʱ��W�����6480��Ԫ��
��x��28ʱ��W�����6480��Ԫ��
�𣺵����۵���Ϊ![]() Ԫʱ��ÿ�����������������������
Ԫʱ��ÿ�����������������������![]() Ԫ
Ԫ