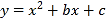题目内容
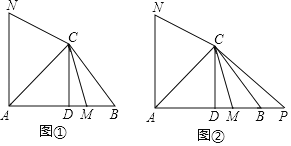
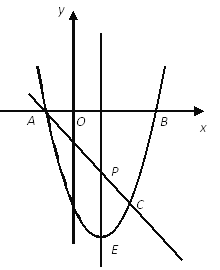
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
【答案】(1)抛物线的解析式y=x2-2x-3,直线AC的函数解析式是y=-x-1;(2)PE的最大值=![]() ;
;
(3)F点的坐标是(-3,0),(1,0),(4-![]() ,0),(4+
,0),(4+![]() ,0).
,0).
【解析】
试题(1)A(-1,0),B(3,0),C(2,-3),该二次函数与x轴交点计算得到
即:![]() ,故A(-1,0)C(2,-3)
,故A(-1,0)C(2,-3)
故:直线AC解析式:y=-x-1 3分
(2)设P(x,-x-1),E(x,x2-2x-3),(![]() )
)
PE=-x2+x+2=-(x-![]() )2+
)2+![]()
![]() ,最大值为
,最大值为![]() 5分
5分
(3)四个点F1(1,0);F2(4+![]() ,0); F3(4-
,0); F3(4-![]() ,0);F4(-3,0) 4分
,0);F4(-3,0) 4分

练习册系列答案
相关题目
【题目】已知卖出的糖果数量x(kg)与售价y(元)的关系如下表:
数量x(kg) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 |
(1)这个表格反映了哪两个变量之间的关系?它们的关系式是什么?
(2)若某顾客付了14.7元,则他购买了多少千克的糖果?