题目内容
【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:![]() ;
;
(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
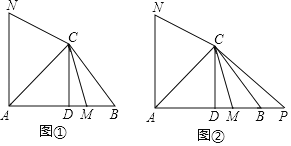
【答案】(1)证明见解析;(2)证明见解析;(3)当AC=2BD时,对于满足条件的任意点N,AN=CP始终成立,证明见解析.
【解析】
(1)由三角形的内角和定理可求∠ACN=∠AMC=135°-∠ACM;
(2)过点N作NE⊥AC于E,由“AAS”可证△NEC≌△CDM,可得NE=CD,由三角形面积公式可求解;
(3)过点N作NE⊥AC于E,由“SAS”可证△NEA≌△CDP,可得AN=CP.
(1)∵∠BAC=45°,
∴∠AMC=180°﹣45°﹣∠ACM=135°﹣∠ACM.
∵∠NCM=135°,
∴∠ACN=135°﹣∠ACM,∴∠ACN=∠AMC;
(2)过点N作NE⊥AC于E,
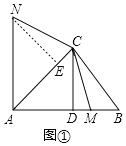
∵∠CEN=∠CDM=90°,∠ACN=∠AMC,CM=CN,
∴△NEC≌△CDM(AAS),
∴NE=CD,CE=DM;
∵S1![]() ACNE,S2
ACNE,S2![]() ABCD,
ABCD,
∴![]() ;
;
(3)当AC=2BD时,对于满足条件的任意点N,AN=CP始终成立,
理由如下:过点N作NE⊥AC于E,
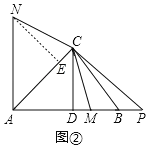
由(2)可得NE=CD,CE=DM.
∵AC=2BD,BP=BM,CE=DM,
∴AC﹣CE=BD+BD﹣DM,
∴AE=BD+BP=DP.
∵NE=CD,∠NEA=∠CDP=90°,AE=DP,
∴△NEA≌△CDP(SAS),
∴AN=PC.

练习册系列答案
相关题目