题目内容
【题目】解答下列各题
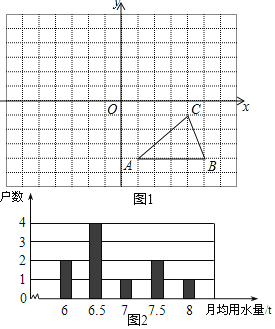
(1)如图1,方格纸中的每个小方格都是边长为1个单位长的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①作出△ABC关于x轴对称的△A1B1C1;
②如果P点的纵坐标为3,且P点到直线AA的距离为5,请直接写出点P的坐标.
(2)我国是世界上严重缺水的国家之一为了倡导“节约用水,从我做起”,小丽同学在她家所在小区的200住户中,随机调查了10个家庭在2019年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数;
②以上面的样本平均数为依据,自来水公司按2019年该小区户月均用水量下达了2020年的用水计划(超计划要执行阶梯式标准收费)请计算该小区2020年的计划用水量.
【答案】(1)①详见解析;②点P的坐标为(﹣4,3)或(6,3);(2)①6.8t;②该小区2020年的计划用水量应为16320t.
【解析】
(1)①由轴对称的性质先确定点A1,B1,C1的坐标,再描点,连线即可;
②由P点到直线AA的距离为5,可知点P的横坐标为﹣4或6,由其纵坐标为3,即可写出点P坐标;
(2)①根据加权平均数的计算方法求解即可;
②可将①中所求10个样本数据的平均数乘以12个月,再乘以200户即可.
解:(1)①如图1,△A1B1C1即为所求;
②如图1,点P的坐标为(﹣4,3)或(6,3);

(2)①(6×2+6.5×4+7×1+7.5×2+8×1)÷10=6.8t,
∴这10个样本数据的平均数为6.8t;
②6.8×12×200=16320t,
∴该小区2020年的计划用水量应为16320t.

练习册系列答案
相关题目