题目内容
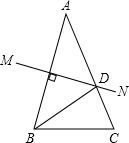
在△ABC中，AB=AC，∠A=36°，BD是∠ABC的平分线，则图中共有______个等腰三角形．
∵AB=AC，∠A=36°，
∴∠ABC=∠C=
（180°-36°）=72°，
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD=
∠ABC=36°，
∴∠BDC=∠A+∠ABD=72°=∠C，
∴BD=BC，AD=BD，
∵AB=AC，
∴等腰三角形有：△ABC，△ADB，△BDC3个．
故答案为：3．
∴∠ABC=∠C=
| 1 |
| 2 |
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD=
| 1 |
| 2 |
∴∠BDC=∠A+∠ABD=72°=∠C，
∴BD=BC，AD=BD，
∵AB=AC，
∴等腰三角形有：△ABC，△ADB，△BDC3个．
故答案为：3．
练习册系列答案
相关题目
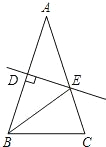
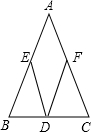
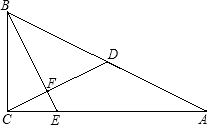于点E，与射线CD相交于点F．
