题目内容
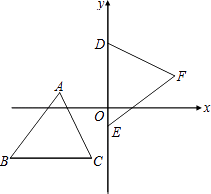
【题目】如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE= ![]() DB,作EF⊥DE并截取EF=DE,连结AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )
DB,作EF⊥DE并截取EF=DE,连结AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( ) 
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y=﹣ ![]()
【答案】A
【解析】解:作FG⊥BC于G, 
∵∠DEB+∠FEC=90°,∠DEB+∠BDE=90°;
∴∠BDE=∠FEG,
在△DBE与△EGF中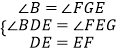
∴△DBE≌△EGF,
∴EG=DB,FG=BE=x,
∴EG=DB=2BE=2x,
∴GC=y﹣3x,
∵FG⊥BC,AB⊥BC,
∴FG∥AB,
CG:BC=FG:AB,
即 ![]() =
= ![]() ,
,
∴y=﹣ ![]() .
.
故选:A.
作FG⊥BC于G,依据已知条件求得△DBE≌△EGF,得出FG=BE=x,EG=DB=2x,然后根据平行线的性质即可求得.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目