题目内容
【题目】九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:tan60°=1.732,tan30°=0.577, ![]() =1.732,
=1.732, ![]() =1.414.
=1.414.
【答案】
(1)
解:∵BD=BC,
∴∠CDB=∠DCB,
∴∠α=2∠CDB=2×38°=76°
(2)
解:如图2,设EF的中点为M,过M作MN⊥BF,垂足为点N,
过点E作EH⊥BF,垂足为点H,

∵MN∥EH,MN=1.9,
∴EH=2MN=3.8(米),
∴E点离地面FB的高度是3.8米
(3)
解:如图3,延长AE交直线PB于点C,
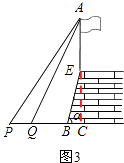
设AE=x,则AC=x+3.8,
∵∠APB=45°,
∴PC=AC=x+3.8,
∵PQ=4,
∴CQ=x+3.8﹣4=x﹣0.2,
∵tan∠AQC= ![]() =tan60°=
=tan60°= ![]() ,
,
∴ ![]() =
= ![]() ,
,
x= ![]() ≈5.7,
≈5.7,
∴AE≈5.7(米).
答;旗杆AE的高度约是5.7米
【解析】(1)根据∠α=2∠CDB即可得出答案;(2)设EF的中点为M,过M作MN⊥BF,垂足为点N,过点E作EH⊥BF,垂足为点H,根据EH=2MN即可求出E点离地面FB的高度;(3)延长AE,交PB于点C,设AE=x,则AC=x+3.8,CQ=x﹣0.2,根据 ![]() =
= ![]() ,得出x+3.8x﹣0.2=3,求出x即可.
,得出x+3.8x﹣0.2=3,求出x即可.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如表:
质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点). 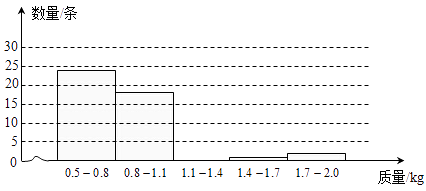
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).