题目内容
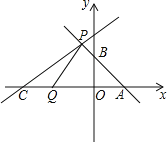
【题目】如图,在![]() 中,斜边
中,斜边![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,
,![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 的延长线与点
的延长线与点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,现有不列结论:①
,现有不列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中正确的个数是( )
,其中正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据线段垂直平分线和角平分线的性质,利用HL可证得①正确;因为∠EAC=45![]() ,而∠ACB不一定是45
,而∠ACB不一定是45![]() ,内错角不相等,因而②错误;利用①的结论结合三角形内角和定理证得∠BEC=∠BAC=90
,内错角不相等,因而②错误;利用①的结论结合三角形内角和定理证得∠BEC=∠BAC=90![]() ,说明③正确;可证明
,说明③正确;可证明![]() 与
与![]() 不全等,说明④错误;可证得四边形AGEM为正方形,利用①的结论结合等量代换,即可证得⑤正确.
不全等,说明④错误;可证得四边形AGEM为正方形,利用①的结论结合等量代换,即可证得⑤正确.
∵DE是BC的垂直平分线,
∴EB=EC,
∵AE是∠BAC的外角平分线,即AE是∠CAM的平分线,且EM⊥AM,EG⊥AC,
∴EM= EG,
∴![]() ,故①正确;
,故①正确;
∵∠BAC=∠MAC=90![]() ,AE是∠CAM的平分线,
,AE是∠CAM的平分线,
∴∠EAM=∠EAC=45![]() ,
,
而∠ACB不是45![]() ,
,
∴AE与BC不平行,故②错误;
∵![]() (HL),
(HL),
∴∠ABN=∠ECN,
又∠ANB=∠ENC,
∴∠BEC=∠BAC=90![]() ,故③正确;
,故③正确;
∵![]() ,
,
∴∠ABE=∠ECF,
∵∠BEC=90![]() ,DE是BC的垂直平分线,
,DE是BC的垂直平分线,
∴EB=EC,∠FEC=45![]() ,
,
∵∠EAM=45![]() ,直线MA与直线EB相交,
,直线MA与直线EB相交,
∴∠AEB![]() 45
45![]() ,
,
∴![]() 与
与![]() 不全等,
不全等,
∴![]() 不成立,故④错误;
不成立,故④错误;
∵∠MAC=90![]() ,EM⊥AM,EG⊥AC,EM= EG,
,EM⊥AM,EG⊥AC,EM= EG,
∴四边形AGEM为正方形,
∴EG=AG=AM,
∵![]() ,
,
∴BM=CG,
∴AC=AG+CG=AG+BM=AG+AM+AB=AB+2EG,故⑤正确;
综上,①③⑤正确,共3个.
故选:B.

练习册系列答案
相关题目