ĢāÄæÄŚČŻ
”¾ĢāÄæ”æij·ē¾°ĒųÄŚµÄ¹«Ā·ČēĶ¼1ĖłŹ¾£¬¾°ĒųÄŚÓŠĆā·ŃµÄ°ą³µ£¬“ÓŌĖŗÓĀėĶ·³ö·¢£¬ŃŲøĆ¹«Ā·æŖĶłŽ¹ŅĀ²Ż×ÆŌ°£¬Ķ¾ÖŠĶ£ææÉśĢ¬ĪÄ»ÆŌ°£ØÉĻĻĀ³µŹ±¼äŗöĀŌ²»¼Ę£©£®µŚŅ»°ą³µÉĻĪē8µć·¢³µ£¬ŅŌŗóĆæøō10·ÖÖÓÓŠŅ»°ą³µ“ÓŌĖŗÓĀėĶ··¢³µ£®Š”“ĻÖÜÄ©µ½øĆ·ē¾°ĒųÓĪĶę£¬ÉĻĪē7:40µ½“ļŌĖŗÓĀėĶ·£¬Ņņ»¹Ć»µ½°ą³µ·¢³µŹ±¼ä£¬ÓŚŹĒ“Ó¾°ĒųŌĖŗÓĀėĶ·³ö·¢£¬ŃŲøĆ¹«Ā·²½ŠŠ25·ÖÖÓŗ󵽓ļÉśĢ¬ĪÄ»ÆŌ°£®ĄėŌĖŗÓĀėĶ·µÄĀ·³Ģ![]() £ØĆ×£©ÓėŹ±¼ä
£ØĆ×£©ÓėŹ±¼ä![]() £Ø·Ö)µÄŗÆŹż¹ŲĻµČēĶ¼2ĖłŹ¾£®
£Ø·Ö)µÄŗÆŹż¹ŲĻµČēĶ¼2ĖłŹ¾£®
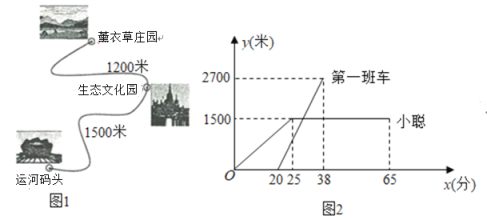
£Ø1£©ĒóµŚŅ»°ą³µĄėŌĖŗÓĀėĶ·µÄĀ·³Ģ![]() £ØĆ×£©ÓėŹ±¼ä
£ØĆ×£©ÓėŹ±¼ä![]() £Ø·Ö£©µÄŗÆŹż±ķ“ļŹ½£®
£Ø·Ö£©µÄŗÆŹż±ķ“ļŹ½£®
£Ø2£©ĒóµŚŅ»°ą³µ“ÓŌĖŗÓĀėĶ·µ½“ļÉśĢ¬ĪÄ»ÆŌ°ĖłŠčµÄŹ±¼ä£®
£Ø3£©Š”“ĻŌŚÉśĢ¬ĪÄ»ÆŌ°ÓĪĶę40·ÖÖÓŗó£¬Ļė×ų°ą³µµ½Ž¹ŅĀ²Ż×ÆŌ°£¬ŌņŠ”“Ļ×īŌēÄܹ»×ųÉĻµŚ¼ø°ą³µ?Čē¹ūĖū×ųÕā°ą³µµ½Ž¹ŅĀ²Ż×ÆŌ°£¬±ČĖūŌŚÉśĢ¬ĪÄ»ÆŌ°ÓĪĶę½įŹųŗóĮ¢¼“²½ŠŠµ½Ž¹ŅĀ²Ż×ÆŌ°ĢįŌēĮĖ¼ø·ÖÖÓ?£Ø¼ŁÉčĆæŅ»°ą³µĖŁ¶Č¾łĻąĶ¬£¬Š”“Ļ²½ŠŠĖŁ¶Č²»±ä£©
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©µŚŅ»°ą³µ“ÓŌĖŗÓĀėĶ·µ½“ļÉśĢ¬ĪÄ»ÆŌ°ĖłŠčŹ±¼ä10·ÖÖÓ£»£Ø3£©±ČĖūŌŚÉśĢ¬ĪÄ»ÆŌ°ÓĪĶę½įŹųŗóĮ¢¼“²½ŠŠµ½Ž¹ŅĀ²Ż×ÆŌ°ĢįŌēĮĖ7·ÖÖÓ£®
£»£Ø2£©µŚŅ»°ą³µ“ÓŌĖŗÓĀėĶ·µ½“ļÉśĢ¬ĪÄ»ÆŌ°ĖłŠčŹ±¼ä10·ÖÖÓ£»£Ø3£©±ČĖūŌŚÉśĢ¬ĪÄ»ÆŌ°ÓĪĶę½įŹųŗóĮ¢¼“²½ŠŠµ½Ž¹ŅĀ²Ż×ÆŌ°ĢįŌēĮĖ7·ÖÖÓ£®
”¾½āĪö”æ
£Ø1£©Éčy=kx+b£¬ŌĖÓĆ“ż¶ØĻµŹż·ØĒó½ā¼“æÉ£»
£Ø2£©°Ńy=1500“śČė£Ø1£©µÄ½āĪöŹ½Ēó³öx¼“æÉ£»
£Ø3£©É芔“Ļ×ųÉĻĮĖµŚn°ą³µ£¬30-25+10£Øn-1£©”Ż40£¬½āµĆn”Ż4.5£¬æɵƊ”“Ļ×ųÉĻĮĖµŚ5°ą³µ£¬ŌŁøł¾Ż”°Ā·³Ģ”¢ĖŁ¶ČÓėŹ±¼äµÄ¹ŲĻµ”±½ā“š¼“æÉ£®
½ā£ŗ£Ø1£©ÓÉĢāŅāµĆ£¬æÉÉčŗÆŹż±ķ“ļŹ½ĪŖ£ŗ![]() £¬
£¬
°Ń![]() £¬
£¬![]() “śČė
“śČė![]() £¬µĆ
£¬µĆ![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬
”ąµŚŅ»°ą³µĄėŌĖŗÓĀėĶ·µÄĀ·³Ģ![]() £ØĆ×£©ÓėŹ±¼ä
£ØĆ×£©ÓėŹ±¼ä![]() £Ø·Ö£©µÄŗÆŹż±ķ“ļĪŖ
£Ø·Ö£©µÄŗÆŹż±ķ“ļĪŖ![]() £»
£»
£Ø2£©°Ń![]() “śČė
“śČė![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬
![]() £Ø·Ö£©£¬
£Ø·Ö£©£¬
”ąµŚŅ»°ą³µ“ÓŌĖŗÓĀėĶ·µ½“ļÉśĢ¬ĪÄ»ÆŌ°ĖłŠčŹ±¼ä10·ÖÖÓ£»
£Ø3£©É芔“Ļ×ųÉĻĮĖµŚ![]() °ą³µ£¬Ōņ
°ą³µ£¬Ōņ
![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬
”ąŠ”“Ļ×ųÉĻĮĖµŚ5°ą³µ£®
µČ³µµÄŹ±¼äĪŖ5·ÖÖÓ£¬×ų°ą³µĖłŠčŹ±¼äĪŖ£ŗ![]() £Ø·Ö£©£¬
£Ø·Ö£©£¬
²½ŠŠĖłŠčŹ±¼ä£ŗ![]() £Ø·Ö£©£¬
£Ø·Ö£©£¬
![]() £Ø·Ö£©£®
£Ø·Ö£©£®
”ą±ČĖūŌŚÉśĢ¬ĪÄ»ÆŌ°ÓĪĶę½įŹųŗóĮ¢¼“²½ŠŠµ½Ž¹ŅĀ²Ż×ÆŌ°ĢįŌēĮĖ7·ÖÖÓ£®

”¾ĢāÄæ”æÉä»÷¶ÓĪŖ“Ó¼×”¢ŅŅĮ½ĆūŌĖ¶ÆŌ±ÖŠŃ”°ĪŅ»ČĖ²Ī¼Ó±ČČü£¬¶ŌĖūĆĒ½ųŠŠĮĖĮł“Ī²āŹŌ£¬²āŹŌ³É¼ØČēĻĀ±ķ£Øµ„Ī»£ŗ»·£©£ŗ
µŚŅ»“Ī | µŚ¶ž“Ī | µŚČż“Ī | µŚĖÄ“Ī | µŚĪå“Ī | µŚĮł“Ī | Ę½¾ł³É¼Ø | ÖŠĪ»Źż | |
¼× | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ¢Ł |
ŅŅ | 10 | 7 | 10 | 10 | 9 | 8 | ¢Ś | 9.5 |
£Ø1£©Ķź³É±ķÖŠĢīæÕ¢Ł £»¢Ś £»
£Ø2£©Ēė¼ĘĖć¼×Įł“Ī²āŹŌ³É¼ØµÄ·½²ī£»
£Ø3£©ČōŅŅĮł“Ī²āŹŌ³É¼Ø·½²īĪŖ![]() £¬ÄćČĻĪŖĶĘ¼öĖ²Ī¼Ó±ČČüøüŗĻŹŹ£¬ĒėĖµĆ÷ĄķÓÉ£®
£¬ÄćČĻĪŖĶĘ¼öĖ²Ī¼Ó±ČČüøüŗĻŹŹ£¬ĒėĖµĆ÷ĄķÓÉ£®