题目内容
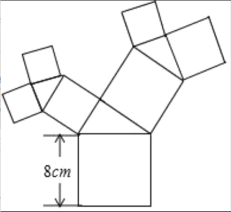
【题目】如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为
，则图中所有正方形的面积的和是___________
．
【答案】192
【解析】
根据正方形的面积公式，连续运用勾股定理，利用四个小正方形的面积和等于最大正方形的面积进而求出即可．
解：如图：
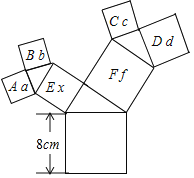
∵所有的三角形都是直角三角形，所有的四边形都是正方形，
∴正方形A的面积=a2，正方形B的面积=b2，正方形C的面积=c2，正方形D的面积=d2，
又∵a2+b2=x2，c2+d2=f2，
∴正方形A、B、C、D的面积和=（a2+b2）+（c2+d2）=x2+f2=82=64（cm2），
则所有正方形的面积的和是：64×3=192（cm2）．
故答案为：192.
练习册系列答案
相关题目
