Question

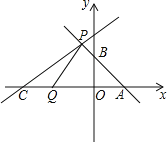
【题目】如图，直线l1：y1＝﹣x+2与x轴，y轴分别交于A，B两点，点P(m，3)为直线l1上一点，另一直线l2：y2＝x+b过点P．

（1）求点P坐标和b的值；

（2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒；

①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；

②直接写出当t为何值时△APQ的面积等于4.5，并写出此时点Q的坐标．

Answer 1

【答案】（1）P的坐标为(﹣1，3)，b＝；（2）①S＝（0＜t＜9）或S＝（t＞9）；②Q的坐标为(﹣1，0)或(5，0)．

【解析】

（1）把P（m，3）的坐标代入直线l1上的解析式即可求得P的坐标，然后根据待定系数法即可求得b；

（2）根据直线l2的解析式得出C的坐标，①根据题意得出AQ＝9﹣t，然后根据S＝AQ|yP|即可求得△APQ的面积S与t的函数关系式；②通过解方程﹣t+＝4.5或t﹣＝4.5，求得t的值，即可求得Q的坐标．

解：（1）∵点P（m，3）为直线l1上一点，

∴3＝﹣m+2，解得m＝﹣1，

∴点P的坐标为（﹣1，3），

把点P的坐标代入y2＝x+b得，3＝×（﹣1）+b，

解得b＝；

（2）∵直线l2的解析式为y＝x+，

∴C点的坐标为（﹣7，0），

①由直线l1：y1＝﹣x+2可知A（2，0），

∴当Q在A、C之间时，AQ＝2+7﹣t＝9﹣t（0＜t＜9），

∴S＝AQ|yP|＝×（9﹣t）×3＝﹣t；

当Q在A的右边时，AQ＝t﹣9（t＞9），

∴S＝AQ|yP|＝×（t﹣9）×3＝t﹣；

即△APQ的面积S与t的函数关系式为S＝﹣t+（0＜t＜9）或S＝t﹣（t＞9）；

②∵S＝4.5，

∴﹣t+＝4.5或t﹣＝4.5

解得t＝6或t＝12，

∴Q的坐标为（﹣1，0）或（5，0）．