题目内容
【题目】在直角坐标系中,A(m,0)为 x 轴负半轴上的点,B(0,n)为 y 轴负半轴上的点.
(1)如图,以 A 点为顶点,AB 为腰在第三象限作等腰 Rt△ABC.若已知 m= 2,n= 4,试求 C 点的坐标;
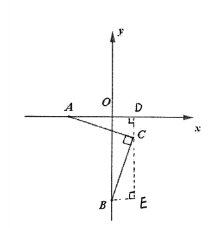
(2)若∠ACB=90°,点 C 的坐标为(4, 4),请在坐标系中画出图形并求 n﹣m 的值.

【答案】(1)C(﹣6,﹣2);(2)画图见解析;-8
【解析】
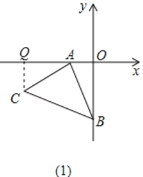
(1)如图(1)作CQ⊥OA于点Q,通过证明△AQC≌△BOA,即可得到CQ=AO=2,AQ=BO=4,从而求 C 点的坐标;
(2)按题意作图,过C作CD⊥x轴,BE⊥y轴,通过证明△ADC≌△CEB,可得AD=CE,再根据AD=4-m,CE=-4-n,代入即可求出n﹣m 的值.
(1)如图(1)作CQ⊥OA于点Q,
∴∠AQC=∠AOB =90°
∵△ABC是等腰直角三角形,
∴AC=AB,∠CAB=90°,
∴∠ACQ+∠CAQ=90°,∠BAO+∠CAQ=90°
∴∠ACQ=∠BAO,
在△AQC与△BOA中,
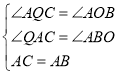 ,
,
∴△AQC≌△BOA,
∴CQ=AO=2,AQ=BO=4.OQ=OA+AQ=6,
∴C(﹣6,﹣2).
(2)如下图所示,过C作CD⊥x轴,BE⊥y轴
∵C的坐标为(4,![]() 4)
4)
∴BE=CD
∵![]()
∴![]()
∴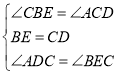
∴△ADC≌△CEB,
∴AD=CE
∵AD=4-m.CE=-4-n
∴4-m=-4-n
∴n-m=-8.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目