题目内容
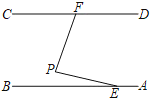
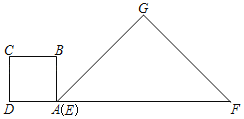
【题目】在△EFG中,∠G=90°,![]() ,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
A.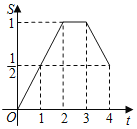 B.
B.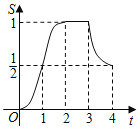
C.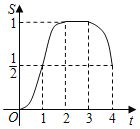 D.
D.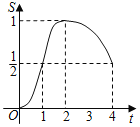
【答案】C
【解析】
分0≤t≤1、1<t≤2、2<t≤3、3<t≤4分别求出函数表达式即可求解.
解:EG=FG=![]() ,则EF=4,
,则EF=4,
①当0≤t≤1时,如图1,设AB交EG于点H,
则AE=t=AH,
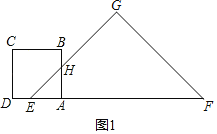
S=![]() ×AE×AH=
×AE×AH=![]() t2,函数为开口向上的抛物线,当t=1时,y=
t2,函数为开口向上的抛物线,当t=1时,y=![]() ;
;
②当1<t≤2时,如图2,设直线EG交BC于点G,交CD于点H,
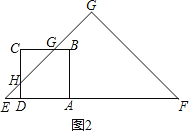
则ED=AE﹣AD=t﹣1=HD,则CH=CD﹣HD=2﹣t=CG,
S=S正方形ABCD﹣S△CGH=1﹣![]() ×CH×CG=1﹣
×CH×CG=1﹣![]() (2﹣t)2,函数为开口向下的抛物线,当t=2时,y=1;
(2﹣t)2,函数为开口向下的抛物线,当t=2时,y=1;
③当2<t≤3时,
S=S正方形ABCD=1,
④当3<t≤4时,
同理可得:S=1﹣![]() (t﹣3)2,为开口向下的抛物线;
(t﹣3)2,为开口向下的抛物线;
故选:C.

练习册系列答案
相关题目
【题目】为了解某区2014年八年级学生的体育测试情况,随机抽取了该区若干名八年级学生的测试成绩进行了统计分析,并根据抽取的成绩等级绘制了如下的统计图表![]() :
:
成绩等级 | A | B | C | D |
人数 | 60 | 10 |
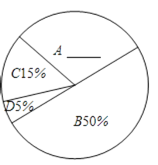
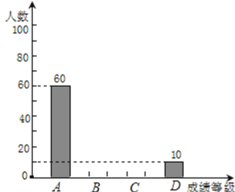
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有______ 名,成绩为B类的学生人数为______ 名,C类成绩所在扇形的圆心角度数为______
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该区约5000名八年级学生体育测试成绩为D类的学生人数.