题目内容
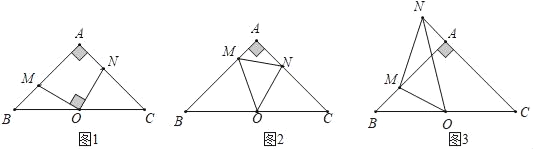
【题目】在Rt△ABC中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线AB、AC于点M、N.
(1)如图1,当α=90°时,求证:AM=CN;
(2)如图2,当α=45°时,问线段BM、MN、AN之间有何数量关系,并证明;
(3)如图3,当α=45°时,旋转∠MON,问线段之间BM、MN、AN有何数量关系?并证明.
【答案】(1)证明见解析;(2)BM=AN+MN,理由见解析;(3)MN=AN+BM.理由见解析.
【解析】
(1)根据题意AB=AC,∠BAC=90°,得出![]() 是一个等腰直角三角形,再根据三线合一得出OA=OB=OC,从而∠ABO=∠ACO=∠BAO=∠CAO=45°,且AO⊥BC,从而得出∠MON=∠AOC=90°,再又因为等角的余角相等,所以∠AOM=∠CON,所以通过证明△AOM≌△CON得出AM=CN
是一个等腰直角三角形,再根据三线合一得出OA=OB=OC,从而∠ABO=∠ACO=∠BAO=∠CAO=45°,且AO⊥BC,从而得出∠MON=∠AOC=90°,再又因为等角的余角相等,所以∠AOM=∠CON,所以通过证明△AOM≌△CON得出AM=CN
(2)根据题意,在BA上截取BG=AN,连接GO,AO,先证明△BGO≌△AON,再证明△GMO≌△NMO得出GM=MN,从而证明出BM=AN+MN
(3)根据题意,过点O作OG⊥ON,连接AO,先证明△NAO≌△GBO,得到AN=
GB,GO=ON,再证明△MON≌△MOG得到MN=MG,从而进一步证明出MN=AN+BM
证明:(1)如图1,连接OA,
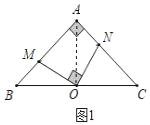
∵AB=AC,∠BAC=90°,OB=OC,
∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,
∴∠MON=∠AOC=90°,
∴∠AOM=∠CON,且AO=CO,∠BAO=∠ACO=45°,
∴△AOM≌△CON(ASA)
∴AM=CN;
(2)BM=AN+MN,
理由如下:如图2,在BA上截取BG=AN,连接GO,AO,
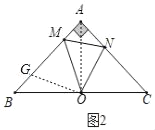
∵AB=AC,∠BAC=90°,OB=OC,
∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,
∵BG=AN,∠ABO=∠NAO=45°,AO=BO,
∴△BGO≌△AON(SAS)
∴OG=ON,∠BOG=∠AON,
∵∠MON=45°=∠AOM+∠AON,
∴∠AOM+∠BOG=45°,且∠AOB=90°,
∴∠MOG=∠MON=45°,且MO=MO,GO=NO,
∴△GMO≌△NMO(SAS)
∴GM=MN,
∴BM=BG+GM=AN+MN;
(3)MN=AN+BM,
理由如下:如图3,过点O作OG⊥ON,连接AO,
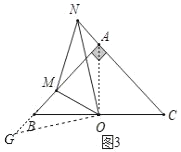
∵AB=AC,∠BAC=90°,OB=OC,
∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,
∴∠GBO=∠NAO=135°,
∵MO⊥GO,
∴∠NOG=90°=∠AOB,
∴∠BOG=∠AON,且AO=BO,∠NAO=∠GBO,
∴△NAO≌△GBO(ASA)
∴AN=GB,GO=ON,
∵MO=MO,∠MON=∠GOM=45°,GO=NO,
∴△MON≌△MOG(SAS)
∴MN=MG,
∵MG=MB+BG,
∴MN=AN+BM.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案