题目内容
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:
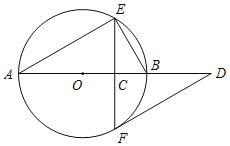
如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C;
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点;
(3)作直线PA,PB.所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_____;由此可证明直线PA,PB都是⊙O的切线,其依据是_____.
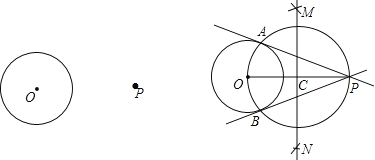
【答案】直径所对的圆周角是直角 经过半径外端,且与半径垂直的直线是圆的切线.
【解析】
分别利用圆周角定理以及切线的判定方法得出答案.
解:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是:直径所对的圆周角是直角;
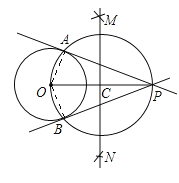
由此可证明直线PA,PB都是⊙O的切线,其依据是:经过半径外端,且与半径垂直的直线是圆的切线.
故答案为:直径所对的圆周角是直角;经过半径外端,且与半径垂直的直线是圆的切线.

练习册系列答案
相关题目