题目内容
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。
 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。
试题分析:二次函数的图象的平移,左右平移对应横坐标变化:左加右减;上下平移是纵坐标变化:上加下减 。故次函数
 的图象向右平移1个单位,得到
的图象向右平移1个单位,得到 ,再向上平移2个单位,得到
,再向上平移2个单位,得到
点评:二次函数的图象的平移,在平移的过程中要清晰知道是横坐标变化,还是是纵坐标变化,不要混淆。

练习册系列答案
相关题目
 向左平移2个单位,向下平移1个单位后得到二次函数
向左平移2个单位,向下平移1个单位后得到二次函数 的图像,则二次函数
的图像,则二次函数
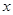 轴的正半轴交于点A,与
轴的正半轴交于点A,与 轴的正半轴交于点B,点C的坐标为(1,0),若抛物线
轴的正半轴交于点B,点C的坐标为(1,0),若抛物线 过A、B两点。
过A、B两点。
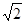 个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?
个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形? 在
在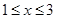 时,
时,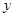 只在
只在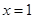 时取得最大值, 则实数
时取得最大值, 则实数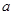 的取值范围是
的取值范围是