题目内容
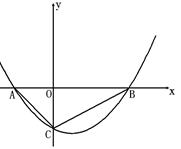
如图,Rt△ABC中,AC=BC=8,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(2,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形B1C1F1E1与△AEF重叠的面积为S.
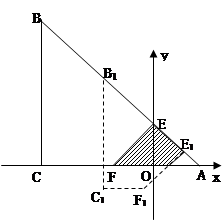
(1)求折痕EF的长;
(2)直接写出S与t的函数关系式及自变量t的取 值范围.
(3)若四边形BCFE平移时,另有一动点H与四边形BCFE同时出发,以每秒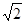 个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?
个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?

(1)求折痕EF的长;
(2)直接写出S与t的函数关系式及自变量t的取 值范围.
(3)若四边形BCFE平移时,另有一动点H与四边形BCFE同时出发,以每秒
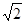 个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?
个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?(1)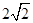 (2)
(2) (
(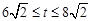 )(3)
)(3)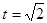 或2
或2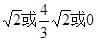
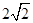 (2)
(2) (
(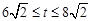 )(3)
)(3)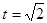 或2
或2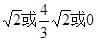
试题分析:1)∵折叠后BE与EA所在直线重合
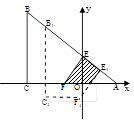
∴EF⊥EA
又Rt△ABC中AC=BC
∴∠CAB=45°
∴EF=EA
∵A(2,0)
∴OA=OE=2 , AE=
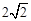
∴折痕EF=
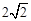
(2)
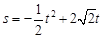 (
(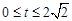 )
)S=4 (
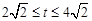 )
)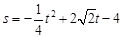 (
( )
) (
(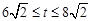 )
) (3)
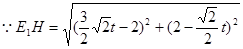
=

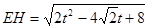
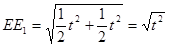
当E1E=EE1时
4t2-8
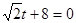
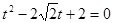
∴t=
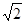
当E1E=EH时,
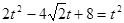

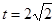
当E1H=EH时

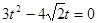
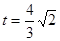 或0
或0综上:
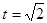 或2
或2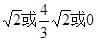
点评:此题将用待定系数法求二次函数解析式、动点问题和最小值问题相结合,有较大的思维跳跃,考查了同学们的应变能力和综合思维能力,是一道好题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
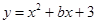 经过点
经过点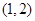 ,那么抛物线的解析式是_____________________。
,那么抛物线的解析式是_____________________。 与x轴交A,B两点(A点在B点左侧),直线
与x轴交A,B两点(A点在B点左侧),直线 与抛物线交于A,C两点,其中C点的横坐标为2.
与抛物线交于A,C两点,其中C点的横坐标为2.
 轴的平行线交抛物线于E点,求线段PE长度的最大值;
轴的平行线交抛物线于E点,求线段PE长度的最大值; 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。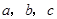 ,用
,用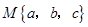 表示这三个数的平均数,用
表示这三个数的平均数,用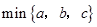 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: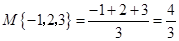 ;
;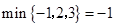 ;
;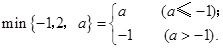
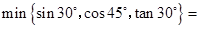 ;
;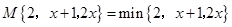 ,求
,求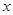 ;
; ,那么 (填
,那么 (填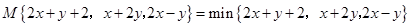 ,则
,则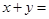 .
.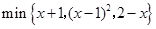 的最大值为 .
的最大值为 .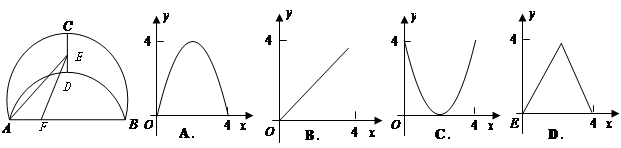
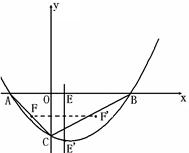
 的图象为抛物线,交x轴于A、B两点,交y轴于C点.其中AC=
的图象为抛物线,交x轴于A、B两点,交y轴于C点.其中AC=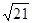 ,BC=
,BC=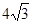 ,
,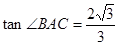 .
.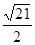 个单位的速度沿着AC向点C匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.过点E作AB的垂线
个单位的速度沿着AC向点C匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.过点E作AB的垂线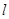 交抛物线于点E′,作点F关于直线
交抛物线于点E′,作点F关于直线