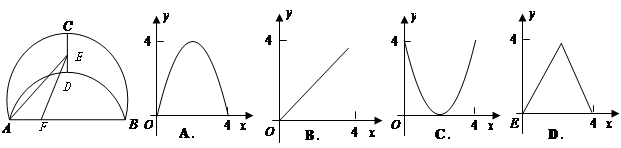题目内容
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.

(1)A(-6,0)B(2,0)C(0,8)
(2)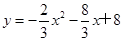 (3)
(3)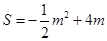 ,
,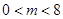
(4)存在
(2)
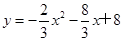 (3)
(3)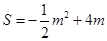 ,
,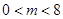
(4)存在
试题分析:(1)解方程
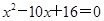 得
得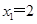 ,
,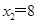
∵点 B 在x轴的正半轴上, 点C在y轴的正半轴上, 且
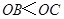
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线
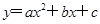 的对称轴是直线
的对称轴是直线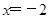
∴由抛物线的对称性可得点A的坐标为(-6,0)
(2)∵点C(0,8)在抛物线
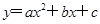 的图象上
的图象上∴c=8,将A(-6,0)、B(2,0)代入表达式,得
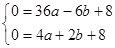 解得
解得 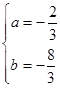
∴所求抛物线的表达式为
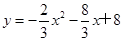
(3)依题意,
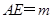 ,则
,则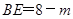 ,
,∵
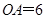 ,
,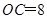 ,∴
,∴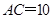
∵EF∥AC ∴△BEF∽△BAC
∴
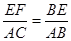 即
即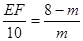
∴EF=
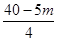
过点F作FG⊥AB,垂足为G,则
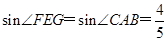
∴
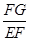 =
=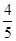 ∴FG=
∴FG=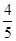 ·
·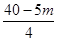 =
=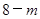
∴
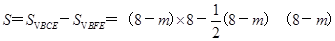
=
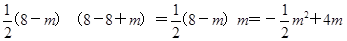
自变量m的取值范围是
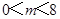
(4)∵
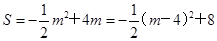 且
且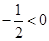 ,
,∴当
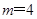 时,S有最大值,
时,S有最大值,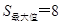
∵
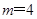 ,∴点E的坐标为(-2,0)
,∴点E的坐标为(-2,0)∴△BCE为等腰三角形.
点评:此类题目难度都不小,学生应该多尝试做此类练习题,一般来讲,都有一定规律在里面,学生可以多做,以求举一反三

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 x2+3x+1的一部分,
x2+3x+1的一部分, (2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这表是
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这表是 的图象下列叙述正确的是( )
的图象下列叙述正确的是( ) =3
=3 有最大值2
有最大值2 与x轴交A,B两点(A点在B点左侧),直线
与x轴交A,B两点(A点在B点左侧),直线 与抛物线交于A,C两点,其中C点的横坐标为2.
与抛物线交于A,C两点,其中C点的横坐标为2.
 轴的平行线交抛物线于E点,求线段PE长度的最大值;
轴的平行线交抛物线于E点,求线段PE长度的最大值; 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 _。 ,
, )为顶点,且过B(
)为顶点,且过B( ,
,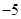 )
)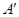 、
、 ,
,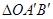 的面积。
的面积。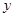 轴的负半轴于点C,则点C的坐标为 ,若二次函数
轴的负半轴于点C,则点C的坐标为 ,若二次函数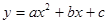 的图像经过点A,C,B.已知点P是该抛物线上的动点,当∠APB是锐角时,点P的横坐标
的图像经过点A,C,B.已知点P是该抛物线上的动点,当∠APB是锐角时,点P的横坐标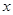 的取值范围是 .
的取值范围是 .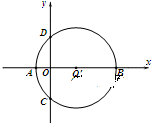
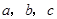 ,用
,用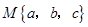 表示这三个数的平均数,用
表示这三个数的平均数,用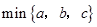 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: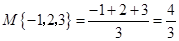 ;
;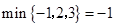 ;
;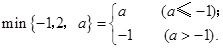
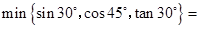 ;
;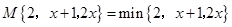 ,求
,求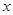 ;
; ,那么 (填
,那么 (填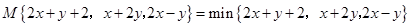 ,则
,则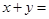 .
.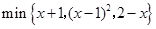 的最大值为 .
的最大值为 .