题目内容
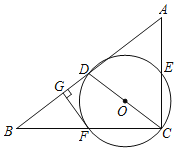
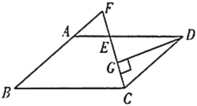
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,
,![]() ,则
,则![]() 的周长为_______.
的周长为_______.
【答案】8
【解析】
由平行四边形的性质和角平分线得出∠F=∠FCB,证出BF=BC=9,同理得到DE=CD=6,利用勾股定理求得CG=EG=2,再利用平行线分线段成比例定理求得EF的长,即可得出结果.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=9,CD=AB=6,
∴∠F=∠DCF,
∵CF平分∠BCD,
∴∠FCB=∠DCF,
∴∠F=∠FCB,
∴![]() 是等腰三角形,
是等腰三角形,
∴BF=BC=9,
∴AF=BF-AB=9-6=3,
同理:DE=CD=6,
∴![]() 是等腰三角形,
是等腰三角形,
∴AE=AD-DE=9-6=3,
∵DG⊥CF,
∴CG=EG,∠DGC=90![]() ,
,
∵![]() ,即
,即![]() ,
,
∴CG=2,CE=2CG=4,
∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥BC,
∴![]() ,即
,即![]() ,
,
解得:EF=2,
∴![]() 的周长为:AF+ AE+ EF=3+3+2=8.
的周长为:AF+ AE+ EF=3+3+2=8.
故答案为:8.

 名校课堂系列答案
名校课堂系列答案【题目】某学校初一、初二年级各有500名学生,为了解两个年级的学生对消防安全知识的掌握情况,学校从初一、初二年级各随机抽取20名学生进行消防安全知识测试,满分100分,成绩整理分析过程如下,请补充完整:
(收集数据)
初一年级20名学生测试成绩统计如下:
78 56 74 81 95 75 87 70 75 90 75 79 86 60 54 80 66 69 83 97
初二年级20名学生测试成绩不低于80,但是低于90分的成绩如下:
83 86 81 87 80 81 82
(整理数据)按照如下分数段整理、描述两组样本数据:
成绩 |
|
|
|
|
|
初一 | 2 | 3 | 7 | 5 | 3 |
初二 | 0 | 4 | 5 | 7 | 4 |
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 76.5 | 76.5 |
| 132.5 |
初二 | 79.2 |
| 74 | 100.4 |
(1)直接写出![]() ,
,![]() 的值;
的值;
(2)根据抽样调查数据,估计初一年级消防安全知识测试成绩在70分及其以上的大约有多少人?
(3)通过以上分析,你认为哪个年级对消防安全知识掌握得更好,并说明推断的合理性.