题目内容
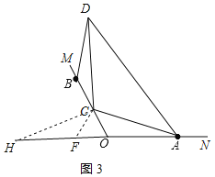
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.
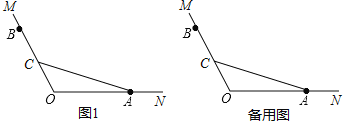
(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
【答案】(1)见解析;(2)①见解析;②见解析;(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由见解析
【解析】
(1)根据题意即可补全图形;
(2)①由旋转得∠ACD=120°,由三角形内角和得出∠DCB+∠ACO=60°,∠OAC+∠ACO=60°,即可得出结论;
②在OA上截取OE=OC,连接CE,则∠OEC=∠OCE=![]() (180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;
(180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;
(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH,在OH上截取OF=OC,连接CF、CH,则FH=OA,∠COF=180°﹣∠MON=60°,得出△OFC 是等边三角形,则CF=OC,∠CFH=∠COA=120°,由SAS证得△CFH≌△COA,得出∠H=∠OAC,由三角形外角性质得出∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,则∠DCH=60°+∠H+∠DCB=60°+2∠OAC,由CA=CD,∠ACD=120°,得出∠CAD=30°,即可得出∠DCH=2∠DAH.
解:(1)根据题意补全图形,如图1所示:
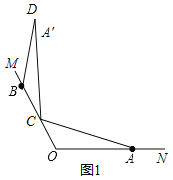
(2)证明:①由旋转得:∠ACD=120°,
∴∠DCB+∠ACO=180°﹣120°=60°,
∵∠MON=120°,
∴∠OAC+∠ACO=180°﹣120°=60°,
∴∠OAC=∠DCB;
②在OA上截取OE=OC,连接CE,如图2所示:
则∠OEC=∠OCE=![]() (180°﹣∠MON)=
(180°﹣∠MON)=![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
∴∠AEC=180°﹣∠OEC=180°﹣30°=150°,
由旋转得:∠CBD=150°,
∴∠AEC=∠CBD,
∵OA=OB,OE=OC,
∴AE=BC,在△AEC和△CBD中,
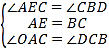 ,
,
∴△AEC≌△CBD(ASA),
∴CD=CA;
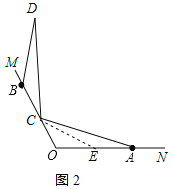
(3)解:猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由如下:
在OH上截取OF=OC,连接CF、CH,如图3所示:
则FH=OA,∠COF=180°﹣∠MON=180°﹣120°=60°,
∴△OFC 是等边三角形,
∴CF=OC,∠CFH=∠COA=120°,
在△CFH和△COA中,
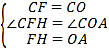 ,
,
∴△CFH≌△COA(SAS),
∴∠H=∠OAC,
∴∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,
∴∠DCH=60°+∠H+∠DCB=60°+2∠OAC,
∵CA=CD,∠ACD=120°,
∴∠CAD=30°,
∴∠DCH=2(∠CAD+∠OAC)=2∠DAH.