题目内容
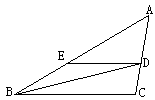
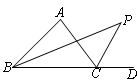
如图．Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，D是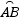
的中点，CD与AB的交点为E，则
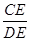等于（ ）
的中点，CD与AB的交点为E，则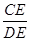等于（ ）| A．4 | B．3.5 | C．3 | D．2.8 |
C
利用垂径定理的推论得出DO⊥AB，AF=BF，进而得出DF的长和△DEF∽△CEA，再利用相似三角形的性质求出即可．
解：连接DO，交AB于点F，
∵D是的中点，∴DO⊥AB，AF=BF，
∵AB=4，∴AF=BF=2，∴FO是△ABC的中位线，AC∥DO，
∵BC为直径，AB=4，AC=3，∴BC=5，∴DO=2.5，
∴DF=2.5﹣1.5=1，
∵AC∥DO，∴△DEF∽△CEA，
∴=
，
∴=
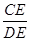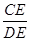=3．
故选C．
解：连接DO，交AB于点F，
∵D是
的中点，∴DO⊥AB，AF=BF，∵AB=4，∴AF=BF=2，∴FO是△ABC的中位线，AC∥DO，
∵BC为直径，AB=4，AC=3，∴BC=5，∴DO=2.5，
∴DF=2.5﹣1.5=1，
∵AC∥DO，∴△DEF∽△CEA，
∴
=，∴
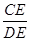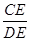==3．故选C．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
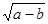+|a?3
|＝0．C为AB的中点，P是线段AB上一动点，D是x轴正半轴上一点，且PO=PD，DE⊥AB于E．
