题目内容
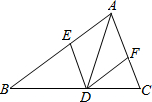
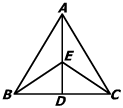
如图,已知:D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE.
证明:在△AEB和△AEC中,
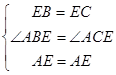
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE(第二步)
问:上面证明过程是否正确?若正确,请写出每一步推理根据;若不正确,请指出错在哪一步?并写出你认为正确的推理过程;

证明:在△AEB和△AEC中,
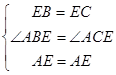
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE(第二步)
问:上面证明过程是否正确?若正确,请写出每一步推理根据;若不正确,请指出错在哪一步?并写出你认为正确的推理过程;
不正确,推理过程见解析;
试题分析:上面证明过程不正确,因为没有正确理解全等三角形的判定方法,SAS指的是两边一角且角为这两边的夹角,所以上面证明过程不正确.这就要求我们要真正理解且正确运用全等三角形的判定方法.
试题解析:上面证明过程不正确;错在第一步.正确过程如下:
在△BEC中,
∵BE=CE
∴∠EBC=∠ECB
又∵∠ABE=∠ACE
∴∠ABC=∠ACB
∴AB=AC.
在△AEB和△AEC中,AE=AE,BE=CE,AB=AC
∴△AEB≌△AEC(SSS)
∴∠BAE=∠CAE.
考点: 全等三角形的判定与性质.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目