Question

【题目】如图，在△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为1，l2，l3之间的距离为2，过点A作AE⊥l3于点E，求BE的长．

Answer 1

【答案】3

【解析】试题分析：过点C作CF⊥l3于点F.根据条件易证△AEB≌△BFC，由全等三角形的性质即可得BE＝CF，从而求得答案.

试题解析：

过点C作CF⊥l3于点F.

∵l1，l2之间的距离为1，l2，l3之间的距离为2，AE⊥l3，CF⊥l3，

∴CF＝3，∠AEB＝∠BFC＝90°.

∴∠EAB＋∠ABE＝90°.

∵∠ABC＝90°，

∴∠ABE＋∠FBC＝90°.

∴∠EAB＝∠FBC.

在△AEB和△BFC中，∵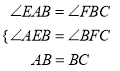

∴△AEB≌△BFC(AAS)．

∴BE＝CF＝3.