Question

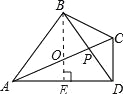
【题目】如图，在四边形ABCD中，∠ABC=∠ADC=90°，对角线AC、BD交于点P，且AB=BD，AP=4PC=4，则cos∠ACB的值是 ．

Answer 1

【答案】.

【解析】

试题分析：如图：作BE⊥AD于E，交AC于O，则BE∥CD，由AB=BD得E是AD的中点，因此OE是△ACD的一条中位线，从而O是AC的中点，以O为圆心，OA为半径作圆，则由∠ABC=∠ADC=90°可知该圆经过A、B、C、D四点，易知 AP=4，PC=1，AC=AP+PC=5，因此，OA=OC=2.5．OP=OC﹣PC=1.5，由BE∥CD得，BP：PD=OP：PC=1.5，因此BP=1.5PD，从而 AB=BD=BP+PD=2.5PD，由相交弦定理得 BPPD=APPC=4，即 1.5PD2=4，因此 PD2=，从而 AB2=（2.5PD）2=6.25PD2=，由勾股定理得BC2=AC2﹣AB2=52﹣=，因此 BC=，∴cos∠ACB=BC：AC=．