题目内容
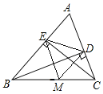
【题目】如图,已知BD、CE是△ABC的高,M是BC边上的中点,若△EMD是等腰直角三角形,则∠A=________°
【答案】45
【解析】
首先根据直角三角形斜边上的中线等于斜边的一半,得出BM=EM=CM=DM,进而得出∠ABC=∠BEM,∠ACB=∠CDM,又根据△EMD是等腰直角三角形,得出∠EMD=90°,通过等量转换,即可得出∠A.
∵BD、CE是△ABC的高,M是BC边上的中点,
∴BM=EM=CM=DM,
∴∠ABC=∠BEM,∠ACB=∠CDM,
又∵△EMD是等腰直角三角形,
∴∠EMD=90°
∴∠BME+∠CMD=90°=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(180°-∠A)
∴∠A=45°

练习册系列答案
相关题目