题目内容
【题目】如图(1)所示为一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示.已知展开图中每个正方形的边长为1:
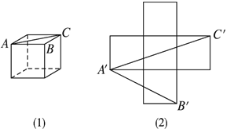
(1)在展开图(2)中可画出最长线段的长度为 ,在平面展开图(2)中这样的最长线段一共能画出 条。
(2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系,并说明理由。
【答案】(1)![]() ,4(2)∠A′B′C′=∠ABC,理由详见解析
,4(2)∠A′B′C′=∠ABC,理由详见解析
【解析】
(1)最长线段应为最大的长方形对角线A′C′长度,根据勾股定理求出长度即可.最大长方形有两个,每一个的对角线有两条,共四条.
(2)连接B′C′,证明三角形全等,利用全等三角形对应角相等的性质,得到∠A′B′C′等于90 °.
(1)由图可知最长的线段应该为最大正方形的对角线,即A′C′的长度,根据勾股定理可得A′C′=![]() .
.
展开图中这样的长方形有2个,每一个长方形有对角线2条,则图(2)中这样的最长线段一共能画出4条.
(2)
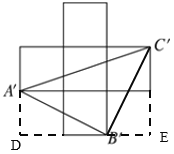
如图所示:
在直角三角形A′B′D与直角三角形C′B′E中,有
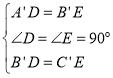
∴![]() (SAS)
(SAS)
∴∠A′B′D=∠B′C′E
又∠B′C′E+∠C′B′E=90°
∴∠A′B′D+∠C′B′E=90°
即∠A′B′C′=90°
而∠ABC=90°
∴∠A′B′C′=∠ABC

练习册系列答案
相关题目