题目内容
【题目】△ABC,AB=AC,AC的垂直平分线与AB所在直线相交所得的锐角为40°,∠C=______.
【答案】65°或25°
【解析】
当△ABC为锐角三角形时,设AC的垂直平分线交线段AB于点D,交AC于点E,在Rt△ADE中可求得∠A,再由三角形内角和定理可求得∠C;当△ABC为钝角三角形时,设AC的垂直平分线交AC于点E,交直线AB于点D,则可求得△CAB的外角,再利用外角的性质可求得∠C,可求得答案.
解:当△ACB为锐角三角形时,如图1,设AC的垂直平分线交线段AB于点D,交AC于点E,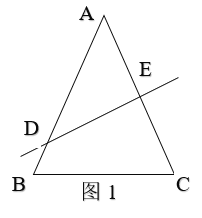
∵∠ADE=40°,DE⊥AC,
∴∠A=90°-40°=50°,
∵AC=AB,
∴∠C=![]() (180°-∠A)=65°;
(180°-∠A)=65°;
当△ABC为钝角三角形时,如图2,设AC的垂直平分线交AC于点E,交AB于点D,
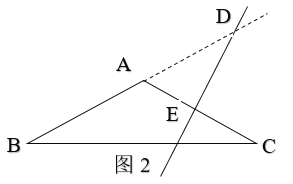
∵∠ADE=40°,DE⊥AC,
∴∠DAC=50°,
∵AC=AB,
∴∠C=∠B,
∵∠C+∠B=∠DAC,
∴∠C=25°;
故答案为: 65°或25°,

练习册系列答案
相关题目
【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.