Question

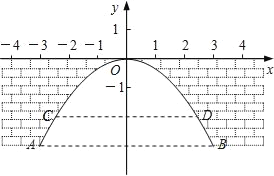
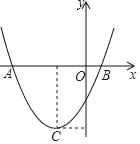
【题目】如图，二次函数y＝ax2+bx+c（a≠0）的图象的顶点C的坐标为（﹣1，﹣3），与x轴交于A（﹣3，0）、B（1，0），根据图象回答下列问题：

（1）写出方程ax2+bx+c＝0的根；

（2）写出不等式ax2+bx+c＞0的解集；

（3）写出y随x的增大而减少时自变量x的取值范围；

（4）若方程ax2+bx+c＝k有实数根，写出实数k的取值范围．

Answer 1

【答案】（1）x1＝﹣3，x2＝1；（2）x＜﹣3或x＞1；（3）y随x的增大而减少时x＜﹣1；（4）当k≥﹣3时，方程ax2+bx+c＝k有实数根．

【解析】

（1）根据抛物线与x轴的交点的横坐标就是二次方程的两个实数根，可直接得结论；

（2）观察图象，在x轴上方的部分y总大于0；

（3）根据A、B的坐标，确定对称轴方程，结合图象得结论；

（4）利用待定系数法先确定a、b、c的值，根据根的判别式得不等式，解不等式得结论．

（1）∵二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A（﹣3，0）、B（1，0），

∴ax2+bx+c＝0的根为：x1＝﹣3，x2＝1．

（2）因为二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A（﹣3，0）、B（1，0），

观察图象可知：当x＜﹣3或x＞1时，图象总在x轴的上方．

所以不等式ax2+bx+c＞0的解集为：x＜﹣3或x＞1．

（3）因为二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A（﹣3，0）、B（1，0），

所以该图象的对称轴为直线x＝﹣1

由于图象开口向上

所以当x＜﹣1时，y随x的增大而减小．

即y随x的增大而减少时x＜﹣1．

（4）抛物线的顶点C的坐标为（-1，-3），且过A（-3，0）、B（1，0），

所以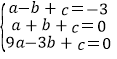

解得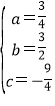

所以抛物线的解析式为y=．

∵方程ax2+bx+c=k有实数根，

即=k有实数根．

∴△===3k+9≥0，

∴k≥-3．

即当k≥-3时，方程ax2+bx+c=k有实数根．