题目内容
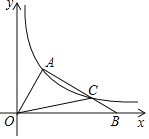
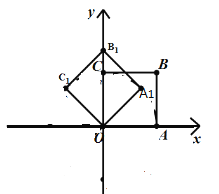
【题目】如图，在平面直角坐标系中，将正方形
绕点
逆时针旋转45°后得到正方形
.依此方式，绕点连续旋转2020次，得到正方形
，如果点
的坐标为
，那么点
的坐标为（ ）
A.
B.
C.
D.
【答案】A
【解析】
根据图形可知：点B在以O为圆心，以OB为半径的圆上运动，由旋转可知：将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，相当于将线段OB绕点O逆时针旋转45°，可得对应点B的坐标，根据规律发现是8次一循环，可得结论．
解：∵四边形OABC是正方形，且OA=
，
∴A1（
，），
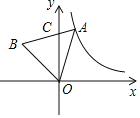
如图，
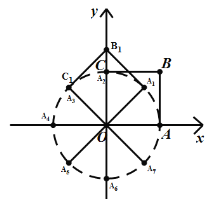
由旋转得：OA=OA1=OA2=OA3=…=，
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，
相当于将线段OA绕点O逆时针旋转45°，依次得到∠AOA1=∠A1OA2=∠A2OA3=…=45°，
∴A1（1，1），A2（0，），A3（
，），A4（
，0）…，
发现是8次一循环，所以2020÷8=252…余4，
∴点A2020的坐标为（，0）；
故选：A.
【题目】随着中央电视台《朗读者》节目的播出，“朗读”为越来越多的同学所喜爱，西宁市某中学计划在全校开展“朗读”活动，为了了解同学们对这项活动的参与态度，随机对部分学生进行了一次调查，调查结果整理后，将这部分同学的态度划分为四个类别：
.积极参与，
.一定参与，
.可以参与，
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
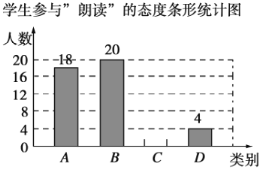
请你根据以上信息，解答下列问题：
（1）
______，
______，并将条形统计图补充完整；
（2）该校有1500名学生，如果“不参与”的人数不超过150人时，“朗读”活动可以顺利开展，通过计算分析这次活动能否顺利开展？
（3）“朗读”活动中，九年级一班比较优秀的四名同学恰好是两男两女，从中随机选取两人在班级进行朗读示范，试用画树状图法或列表法求所选两人都是女生的概率，并列出所有等可能的结果.
【题目】某区在实施居民用水管理前，随机调查了部分家庭（单位：户）去年的月均用水量（单位：t），并将调查数据进行整理，绘制出如下不完整的统计图表：
月均用水量 | 频数 | 频率 |
0≤x＜5 | 6 | 12% |
5≤x＜10 | 12 | 24% |
10≤x＜15 |
| 32% |
15≤x＜20 | 10 | 20% |
20≤x＜25 | 4 |
|
25≤x＜30 | 2 | 4% |
合计 |
| 100% |
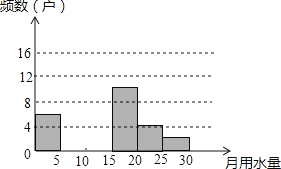
请解答以下问题：
（I）把上面的频数分布表和频数分布直方图补充完整；
（Ⅱ）若该小区有2000户家庭，根据此次随机抽查的数据估计，该小区月均用水量不低于20t的家庭有多少户？
（Ⅲ）为了鼓励节约用水，要确定一个月均用水量的标准，超出该标准的部分按1.5倍价格收费，若要使68%的家庭水费支出不受影响，那么，你觉得家庭月均用水量应定为多少？