题目内容
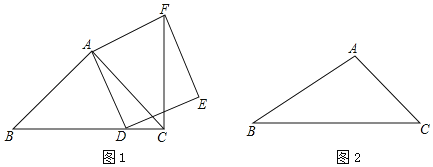
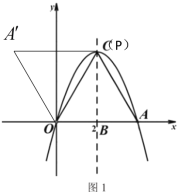
【题目】如图1,过原点的抛物线与![]() 轴交于另一点
轴交于另一点![]() ,抛物线顶点
,抛物线顶点![]() 的坐标为
的坐标为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .
.
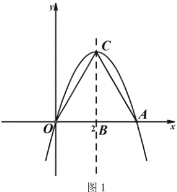
(1)求抛物线的解析式;
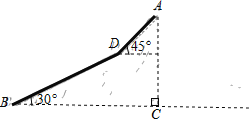
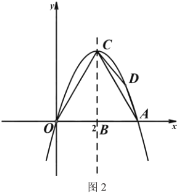
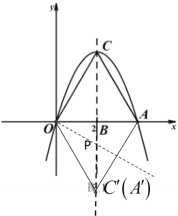
(2)如图2,点![]() 为抛物线上位于第一象限内且在对称轴右侧的一个动点,求使
为抛物线上位于第一象限内且在对称轴右侧的一个动点,求使![]() 面积最大时点
面积最大时点![]() 的坐标;
的坐标;
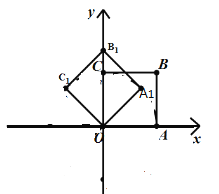
(3)在对称轴上是否存在点![]() ,使得点
,使得点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 满足以点
满足以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形.若存在,请求出点
为顶点的四边形为菱形.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或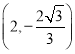
【解析】
(1)设出抛物线的顶点式,将顶点C的坐标和原点坐标代入即可;
(2)先求出点A的坐标,再利用待定系数法求出AC的解析式,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,设
,设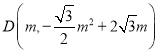 ,则
,则![]() ,然后利用“铅垂高,水平宽”即可求出
,然后利用“铅垂高,水平宽”即可求出![]() 面积与m的关系式,利用二次函数求最值,即可求出此时点D的坐标;
面积与m的关系式,利用二次函数求最值,即可求出此时点D的坐标;
(3)先证出![]() 为等边三角形,然后根据P点的位置和菱形的顶点顺序分类讨论:①当点
为等边三角形,然后根据P点的位置和菱形的顶点顺序分类讨论:①当点![]() 与点
与点![]() 重合时,易证:四边形
重合时,易证:四边形![]() 是菱形,即可求出此时点P的坐标;②作点
是菱形,即可求出此时点P的坐标;②作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,当点
,当点![]() 与点
与点![]() 重合时,易证:四边形
重合时,易证:四边形![]() 是菱形,先求出
是菱形,先求出![]() ,再根据锐角三角函数即可求出BP,从而求出此时点P的坐标.
,再根据锐角三角函数即可求出BP,从而求出此时点P的坐标.
(1)解:设抛物线解析式为![]() ,
,![]()
∵顶点![]()
∴![]()
又∵图象过原点
∴![]() 解出:
解出:![]()
∴![]() 即
即![]()
(2)令![]() ,即
,即![]() ,解出:
,解出:![]() 或
或![]()
∴![]()
设直线AC的解析式为y=kx+b
将点![]() ,
,![]() 的坐标代入,可得
的坐标代入,可得
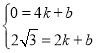
解得: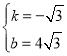
∴![]()
过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,
设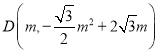 ,则
,则![]()
∴![]()
∴![]()
![]()
∴当![]() 时,
时,![]() 有最大值
有最大值
当![]() 时,
时,![]()
∴![]()
(3)∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]() 为等边三角形
为等边三角形
①当点![]() 与点
与点![]() 重合时,
重合时,![]()
∴四边形![]() 是菱形
是菱形
∴![]()
②作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,
![]()
∴四边形![]() 是菱形
是菱形
∴点![]() 是
是![]() 的角平分线与对称轴的交点,
的角平分线与对称轴的交点,
∴![]() ,
,
∵![]() ,
,![]() .
.
在Rt△OBP中,![]()
∴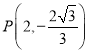
综上所述,点![]() 的坐标为
的坐标为![]() 或
或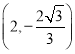

 阅读快车系列答案
阅读快车系列答案【题目】坚持农业农村优先发展,按照产业兴旺、生态宜居的总要求,统筹推进农村经济建设.洛宁县某村出售特色水果(苹果).规定如下:
品种 | 购买数量低于50箱 | 购买数量不低于50箱 |
新红星 | 原价销售 | 以八折销售 |
红富士 | 原价销售 | 以九折销售 |
如果购买新红星40箱,红富士60箱,需付款4300元;如果购买新红星100箱,红富士35箱,需付款4950元.
(1)每箱新红星、红富士的单价各多少元?
(2)某单位需要购置这两种苹果120箱,其中红富士的数量不少于新红星的一半,并且不超过60箱,如何购买付款最少?请说明理由.
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质: .