Question

【题目】某区在实施居民用水管理前，随机调查了部分家庭（单位：户）去年的月均用水量（单位：t），并将调查数据进行整理，绘制出如下不完整的统计图表：

月均用水量	频数	频率
0≤x＜5	6	12%
5≤x＜10	12	24%
10≤x＜15		32%
15≤x＜20	10	20%
20≤x＜25	4
25≤x＜30	2	4%
合计		100%

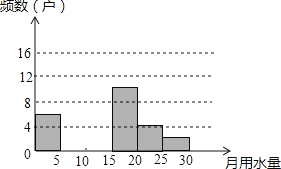
请解答以下问题：

（I）把上面的频数分布表和频数分布直方图补充完整；

（Ⅱ）若该小区有2000户家庭，根据此次随机抽查的数据估计，该小区月均用水量不低于20t的家庭有多少户？

（Ⅲ）为了鼓励节约用水，要确定一个月均用水量的标准，超出该标准的部分按1.5倍价格收费，若要使68%的家庭水费支出不受影响，那么，你觉得家庭月均用水量应定为多少？

Answer 1

【答案】（I）详见解析；（Ⅱ）240；（Ⅲ）15t．

【解析】

（Ⅰ）由0≤x＜5的频数及其频率可得总户数，再根据频率＝频数÷总户数分别求解可得；

（Ⅱ）用总户数乘以样本中20≤x＜25、25≤x＜30的频率和即可得；

（Ⅲ）前三个分组的频率之和为12%+24%+32%＝68%即可得．

（Ⅰ）∵被调查的总数量为6÷12%＝50（户），

∴10≤x＜15的频数为50×32%＝16（户）、20≤x＜25的频率为4÷50＝0.08＝8%，

补全图形如下：

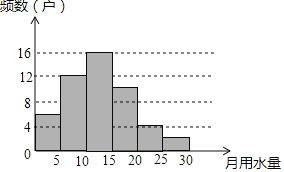
月均用水量	频数	频率
0≤x＜5	6	12%
5≤x＜10	12	24%
10≤x＜15	16	32%
15≤x＜20	10	20%
20≤x＜25	4	8%
25≤x＜30	2	4%
合计	50	100%

（Ⅱ）估计该小区月均用水量不低于20t的家庭有2000×（8%+4%）＝240户；

（Ⅲ）∵前三个分组的频率之和为12%+24%+32%＝68%，

∴家庭月均用水量应定为15t．