题目内容
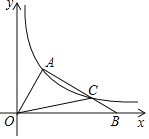
【题目】如图,在平面直角坐标系xOy中,△OAB的边OB在x轴上,过点A的反比例函数y=![]() 的图象交AB于点C,且AC:CB=2:1,S△OAC=
的图象交AB于点C,且AC:CB=2:1,S△OAC=![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.2D.2
C.2D.2![]()
【答案】B
【解析】
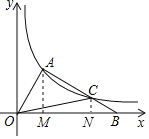
设C(a,b),根据题意则A(![]() a,3b),然后根据S△OAC=S梯形AMNC+S△OAMS△CON=S梯形AMNC,得到
a,3b),然后根据S△OAC=S梯形AMNC+S△OAMS△CON=S梯形AMNC,得到![]() (3b+b)(a
(3b+b)(a![]() a)=
a)=![]() ,即可求得k=ab=
,即可求得k=ab=![]() .
.
设C(a,b),
作AM⊥x轴于M,CN⊥x轴于N,
∴ON=a,CN=b,
∵CN∥AM,
∴△BCN∽△BAM,
∴![]() ,
,
∵AC:CB=2:1,
∴BC:AB=1:3,
∴AM=3CN=3b,
∵点A的反比例函数y=![]() 的图象交AB于点C,
的图象交AB于点C,
∴OMAM=OCN=k,
∴OM=![]() ON=
ON=![]() a,
a,
∵S△OAC=S梯形AMNC+S△OAM﹣S△CON=S梯形AMNC,
∴S梯形AMNC=![]() (3b+b)(a
(3b+b)(a![]() a)=
a)=![]() ,
,
∴k=ab=![]() ,
,
故选:B.

【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润(元/件) | B型利润(元/件) | |
甲店 | 180 | 150 |
乙店 | 120 | 110 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并写出x的取值范围;
(2)若要求总利润超过14960元,有多少种不同分配方案?请列出具体方案;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润,甲店的B型产品以及乙店的A,B型产品的每件利润不变,该公司如何设计分配方案,使总利润达到最大?
【题目】坚持农业农村优先发展,按照产业兴旺、生态宜居的总要求,统筹推进农村经济建设.洛宁县某村出售特色水果(苹果).规定如下:
品种 | 购买数量低于50箱 | 购买数量不低于50箱 |
新红星 | 原价销售 | 以八折销售 |
红富士 | 原价销售 | 以九折销售 |
如果购买新红星40箱,红富士60箱,需付款4300元;如果购买新红星100箱,红富士35箱,需付款4950元.
(1)每箱新红星、红富士的单价各多少元?
(2)某单位需要购置这两种苹果120箱,其中红富士的数量不少于新红星的一半,并且不超过60箱,如何购买付款最少?请说明理由.