题目内容
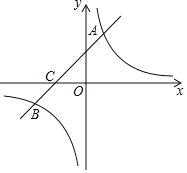
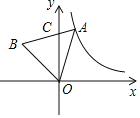
【题目】如图,等边![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数
是反比例函数![]() 图像上的一点,且
图像上的一点,且![]() ,则等边
,则等边![]() 的边长为______.
的边长为______.
【答案】![]()
【解析】
设等边三角形的边长为b,过点A作x轴的平行线交y轴于点M,设AM=a
过点B作y轴的平行线交AM的延长线于点E,过点O作ON⊥AB与点N,AN=![]() AB=
AB=![]() b,ON=
b,ON=![]() b,AN=
b,AN=![]() b,AC=
b,AC=![]() b,则CN=AN-AC=
b,则CN=AN-AC=![]() b,CM∥BE,则
b,CM∥BE,则![]() ,则
,则 ,则AE=3a,可证△ONC∽△AEB,
,则AE=3a,可证△ONC∽△AEB,![]() ,即
,即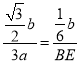 ,解得:BE=
,解得:BE=![]() ,AB2=AE2+BE2,则b2=
,AB2=AE2+BE2,则b2=![]() a2+9a2=
a2+9a2=![]() a2,点A(a,
a2,点A(a,![]() ),则AB2=a2+
),则AB2=a2+![]() ,即可求解.
,即可求解.
设等边三角形的边长为b,过点A作x轴的平行线交y轴于点M,设AM=a
过点B作y轴的平行线交AM的延长线于点E,过点O作ON⊥AB与点N,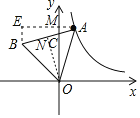
则AN=![]() AB=
AB=![]() b,ON=
b,ON=![]() b,AC=
b,AC=![]() b,
b,
则CN=AN-AC=![]() b,
b,
∵CM∥BE,
∴![]() ,即
,即 ,
,
∴AE=3a,
∵∠OCN=∠ACM=∠ABE,
∴△ONC∽△AEB,
∴![]() ,即
,即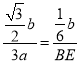 ,
,
解得:BE=![]()
∵AB2=AE2+BE2,即b2=![]() a2+9a2=
a2+9a2=![]() a2,
a2,
∵点A(a,![]() ),
),
则AB2=a2+![]()
解得:a2=3,则b=2![]() ,
,
故答案为2![]()

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目