题目内容
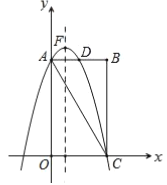
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() 与直线
与直线![]() 相交所得的锐角为60°.点
相交所得的锐角为60°.点![]() 在直线
在直线![]() 上,
上,![]() ,
,![]() 直线
直线![]() ,垂足为点
,垂足为点![]() 且
且![]() ,以
,以![]() 为直径,在
为直径,在![]() 的左侧作半圆
的左侧作半圆![]() ,点
,点![]() 是半圆
是半圆![]() 上任一点.
上任一点.
发现:![]() 的最小值为_________,
的最小值为_________,![]() 的最大值为__________,
的最大值为__________,![]() 与直线
与直线![]() 的位置关系_________.
的位置关系_________.
思考:矩形![]() 保持不动,半圆
保持不动,半圆![]() 沿直线
沿直线![]() 向左平移,当点
向左平移,当点![]() 落在
落在![]() 边上时,求半圆与矩形重合部分的周长和面积.
边上时,求半圆与矩形重合部分的周长和面积.
【答案】![]() , 10 ,
, 10 , ![]() ;
;![]() ,
,![]() .
.
【解析】
发现:先依据勾股定理求得AO的长,然后由圆的性质可得到OM=3,当点M在AO上时,AM有最小值,当点M与点E重合时,AM有最大值,然后过点B作BG⊥l,垂足为G,接下来求得BG的长,从而可证明四边形OBGF为平行四边形,于是可得到OB与直线1的位置关系.
思考:连结OG,过点O作OH⊥EG,依据垂径定理可知GE=2HE,然后在△EOH中,依据特殊锐角三角函数值可求得HE的长,从而得到EG的长,接下来求得∠EOG得度数,依据弧长公式可求得弧EG的长,利用扇形面积减去三角形面积即可得到面积.
解:发现:由题意可知OM=OF=3,AF=8,EF⊥l,
∴OA=![]() .
.
当点M在线段OA上时,AM有最小值,最小值为=![]() .
.
当点M与点E重合时,AM有最大值,最大值=![]() .
.
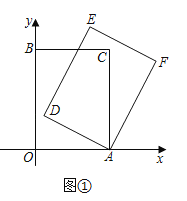
如图1所示:过点B作BG⊥l,垂足为G.
∵∠DAF=60°,∠BAD=90°,
∴∠BAG=30°.
∴GB=![]() AB=3.
AB=3.
∴OF=BG=3,
又∵GB∥OF,
∴四边形OBGF为平行四边形,
∴OB∥FG,即OB∥l.
故答案为:![]() ,10,
,10,![]() ;
;
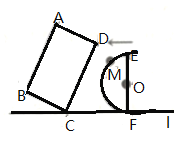
思考:如图2所示:连结![]() ,过点
,过点![]() 作
作![]() ,
,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
弧![]() 的长
的长![]() ,
,
∴半圆与矩形重合部分的周长![]() ,
,
∴![]()
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
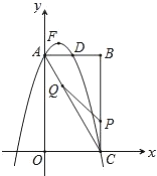
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
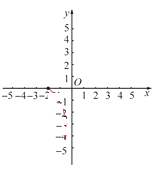
(4)结合函数的图象,写出该函数的一条性质: .